题目内容
已知等差数列{an}满足:a1+a2n-1=2n,(n∈N*),设Sn是数列{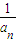 }的前n项和,记f(n)=S2n-Sn,
}的前n项和,记f(n)=S2n-Sn,(1)求an;(n∈N*)
(2)比较f(n+1)与f(n)的大小;(n∈N*)
(3)如果函数g(x)=log2x-12f(n)(其中x∈[a,b])对于一切大于1的自然数n,其函数值都小于零,那么a、b应满足什么条件?
【答案】分析:(1)因为数列{an}为等差数列,所以数列中的每一项均可用首项和公差表示,代入a1+a2n-1=2n,即可求出an.
(2)根据等差数列的通项公式,求出函数f(n)的表达式,再用作差法比较f(n+1)与f(n)的大小.
(3)如果函数g(x)=log2x-12f(n)(其中x∈[a,b])对于一切大于1的自然数n,其函数值都小于零,则log2x-12f(n)<0恒成立,即当x∈[a,b]时,log2x小于12f(n)的最小值,根据f(n)的单调性求出最小值即可.
解答:解:(1)设an=a1+(n-1)d,(n∈N*),由a1+a2n-1=2n,得a1+a1+(2n-1-1)d=2n,
所以an=n
(2)由Sn= +
+ +…+
+…+ =
= +
+ +…+
+…+
f(n)=S2n-Sn=( +
+ +…+
+…+ )-(
)-( +
+ +…+
+…+ )=
)= +
+ +…+
+…+
因为f(n+1)-f(n)=( +
+ +…+
+…+ )-(
)-( +
+ +…+
+…+ )
)
= +
+ -
-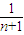
= >0
>0
所以f(n+1)>f(n)
(3)由(2)可知:数列{f(n)}的项的取值是随n的增大而增大,
当n≥2时,f(n)的最小值为f(2)= =
=
由函数y=log2x的性质可知,在区间(0,27)上的函数值恒小于7,
所以a、b应满足条件0<a<b<27.
点评:本题主要考查了函数与数列的综合运用,注意两个知识点的结合.
(2)根据等差数列的通项公式,求出函数f(n)的表达式,再用作差法比较f(n+1)与f(n)的大小.
(3)如果函数g(x)=log2x-12f(n)(其中x∈[a,b])对于一切大于1的自然数n,其函数值都小于零,则log2x-12f(n)<0恒成立,即当x∈[a,b]时,log2x小于12f(n)的最小值,根据f(n)的单调性求出最小值即可.
解答:解:(1)设an=a1+(n-1)d,(n∈N*),由a1+a2n-1=2n,得a1+a1+(2n-1-1)d=2n,
所以an=n
(2)由Sn=
 +
+ +…+
+…+ =
= +
+ +…+
+…+
f(n)=S2n-Sn=(
 +
+ +…+
+…+ )-(
)-( +
+ +…+
+…+ )=
)= +
+ +…+
+…+
因为f(n+1)-f(n)=(
 +
+ +…+
+…+ )-(
)-( +
+ +…+
+…+ )
)=
 +
+ -
-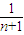
=
 >0
>0所以f(n+1)>f(n)
(3)由(2)可知:数列{f(n)}的项的取值是随n的增大而增大,
当n≥2时,f(n)的最小值为f(2)=
 =
=
由函数y=log2x的性质可知,在区间(0,27)上的函数值恒小于7,
所以a、b应满足条件0<a<b<27.
点评:本题主要考查了函数与数列的综合运用,注意两个知识点的结合.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.