题目内容
设函数f(x)对任意x,y∈R,都f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2,
(1)求证:f(x)是奇函数;
(2)试问在-3≤x≤3时时,f(x)是否有最值?如果有,求出最值;如果没有,说出理由.
(1)求证:f(x)是奇函数;
(2)试问在-3≤x≤3时时,f(x)是否有最值?如果有,求出最值;如果没有,说出理由.
(1)证明:令x=y=0,则有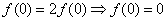 ,
,
令y=-x,则有 ,
,
即 ,
,
∴f(x)是奇函数.
(2)任取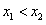 ,则
,则 ,
,
且 ,
,
∴ ,
,
∴y= f(x)在R上为减函数,
因为f(3)为函数的最小值,f(-3)为函数的最大值,
f(3)=f(1)+f(2)=3f(1)=-6,f(-3)=-f(3)=6,
∴函数的最大值为6,最小值为-6.
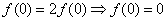 ,
,令y=-x,则有
 ,
,即
 ,
,∴f(x)是奇函数.
(2)任取
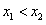 ,则
,则 ,
,且
 ,
,∴
 ,
,∴y= f(x)在R上为减函数,
因为f(3)为函数的最小值,f(-3)为函数的最大值,
f(3)=f(1)+f(2)=3f(1)=-6,f(-3)=-f(3)=6,
∴函数的最大值为6,最小值为-6.

练习册系列答案
相关题目
 对任意x
对任意x 恒成立,则实数m的取值范围是_______
恒成立,则实数m的取值范围是_______