题目内容
如图，已知过原点O从x轴正方向出发顺时针转60°得到射线t，点A（x，y）在射线t上
x＞0，y＜0
，设|OA|＝m；又点B（
，
）在射线y＝0（
＞0）上移动；设点P为第四象限的动点，若
·
＝0，且
·
，
·
，
成等差数列．
（Ⅰ）求动点P的轨迹方程，并说明轨迹C的形状；
（Ⅱ）已知动直线l与曲线C有三个不同的交点M、N，且
∥v，v＝（2，1），设 Q（
，
）为线段MN的中点，求
的取值范围．
答案：
解析：
解析：
解：（Ⅰ） ∵ ∴ 得 ∴ P的轨迹C为以（ （Ⅱ）设 解得 ∴
|
，∴ 
，设
，
，
，
， ∴ 
轴，
，
，
，
，
，
，
，由
，
，
成等差数列．
，即
．
，
）为圆心，半径为
的圆在y轴下方的部分．
，
，
，
，直线
：
代入到轨迹C的方程，消x得：
，由
，
，
，
，又
，
．
练习册系列答案
相关题目
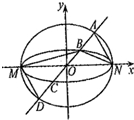（2013•湖北）如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记
x
·
=0，且
·
，
·
，|
|2成等差数列. 
,若直线l与曲线C有两个不同的交点M，N，设线段MN的中点为Q，求点Q的横坐标的取值范围.
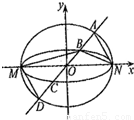如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记
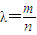，△BDM和△ABN的面积分别为S1和S2．