题目内容
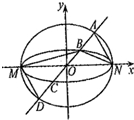 (2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记λ=
(2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记λ=| m | n |
(Ⅰ)当直线l与y轴重合时,若S1=λS2,求λ的值;
(Ⅱ)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.
分析:(Ⅰ)设出两个椭圆的方程,当直线l与y轴重合时,求出△BDM和△ABN的面积S1和S2,直接由面积比=λ列式求λ的值;
(Ⅱ)假设存在与坐标轴不重合的直线l,使得S1=λS2,设出直线方程,由点到直线的距离公式求出M和N到直线l的距离,利用数学转化思想把两个三角形的面积比转化为线段长度比,由弦长公式得到线段长度比的另一表达式,两式相等得到
=
,换元后利用非零的k值存在讨论λ的取值范围.
(Ⅱ)假设存在与坐标轴不重合的直线l,使得S1=λS2,设出直线方程,由点到直线的距离公式求出M和N到直线l的距离,利用数学转化思想把两个三角形的面积比转化为线段长度比,由弦长公式得到线段长度比的另一表达式,两式相等得到
|
| λ+1 |
| λ(λ-1) |
解答: 解:以题意可设椭圆C1和C2的方程分别为
解:以题意可设椭圆C1和C2的方程分别为
C1:
+
=1,C2:
+
=1.其中a>m>n>0,
λ=
.
(Ⅰ)如图1,若直线l与y轴重合,即直线l的方程为x=0,则
S1=
|BD|•|OM|=
a|BD|,
S2=
|AB|•|ON|=
a|AB|,
所以
=
.
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
于是
=
=
=
.
若
=λ,则
=λ,化简得λ2-2λ-1=0,由λ>1,解得λ=
+1.
故当直线l与y轴重合时,若S1=λS2,则λ=
+1.
(Ⅱ)如图2,若存在与坐标轴不重合的直线l,使得S1=λS2,根据对称性,
不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,则
d1=
=
,d2=
=
,所以d1=d2.
又S1=
|BD|d1,S2=
|AB|d2,所以
=
=λ,即|BD|=λ|AB|.
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
=
.
将l的方程分别与C1和C2的方程联立,可求得
xA=
,xB=
根据对称性可知xC=-xB,xD=-xA,于是
=
=
②
从而由①和②可得
=
③
令t=
,则由m>n,可得t≠1,于是由③可得k2=
.
因为k≠0,所以k2>0.于是③关于k有解,当且仅当
>0,
等价于(t2-1)(t2-
)<0,由λ>1,解得
<t<1,
即
<
<1,由λ>1,解得λ>1+
,所以
当1<λ≤1+
时,不存在与坐标轴不重合的直线l,使得S1=λS2;
当λ>1+
时,存在与坐标轴不重合的直线l,使得S1=λS2.
 解:以题意可设椭圆C1和C2的方程分别为
解:以题意可设椭圆C1和C2的方程分别为C1:
| x2 |
| a2 |
| y2 |
| m2 |
| x2 |
| a2 |
| y2 |
| n2 |
λ=
| m |
| n |
(Ⅰ)如图1,若直线l与y轴重合,即直线l的方程为x=0,则
S1=
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
所以
| S1 |
| S2 |
| |BD| |
| |AB| |
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
于是
| |BD| |
| |AB| |
| |yB-yD| |
| |yA-yB| |
| m+n |
| m-n |
| λ+1 |
| λ-1 |
若
| S1 |
| S2 |
| λ+1 |
| λ-1 |
| 2 |
故当直线l与y轴重合时,若S1=λS2,则λ=
| 2 |

(Ⅱ)如图2,若存在与坐标轴不重合的直线l,使得S1=λS2,根据对称性,
不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,则
d1=
| |-ak-0| | ||
|
| ak | ||
|
| |ak-0| | ||
|
| ak | ||
|
又S1=
| 1 |
| 2 |
| 1 |
| 2 |
| S1 |
| S2 |
| |BD| |
| |AB| |
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
| |AD| |
| |BC| |
| λ+1 |
| λ-1 |
将l的方程分别与C1和C2的方程联立,可求得
xA=
| am | ||
|
| an | ||
|
根据对称性可知xC=-xB,xD=-xA,于是
| |AD| |
| |BC| |
| ||
|
| m |
| n |
|
从而由①和②可得
|
| λ+1 |
| λ(λ-1) |
令t=
| λ+1 |
| λ(λ-1) |
| n2(λ2t2-1) |
| a2(1-t2) |
因为k≠0,所以k2>0.于是③关于k有解,当且仅当
| n2(λ2t2-1) |
| a2(1-t2) |
等价于(t2-1)(t2-
| 1 |
| λ2 |
| 1 |
| λ |
即
| 1 |
| λ |
| λ+1 |
| λ(λ-1) |
| 2 |
当1<λ≤1+
| 2 |
当λ>1+
| 2 |
点评:本题考查了三角形的面积公式,考查了点到直线的距离公式,考查了直线与圆锥曲线的关系,该题重点考查了数学转化思想方法和分类讨论的数学思想方法,(Ⅱ)中判断λ的存在性是该题的难题,考查了灵活运用函数和不等式的思想方法.

练习册系列答案
相关题目
 (2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. (2013•湖北)如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
(2013•湖北)如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( ) (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.