题目内容
设M是△ABC中任意一点,且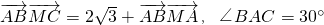 ,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若
,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若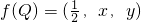 ,则在平面直坐标系中点(x,y)的轨迹是
,则在平面直坐标系中点(x,y)的轨迹是
- A.

- B.

- C.

- D.

B
分析:先求出|AB|•|AC|的值,再求出△ABC的面积等于1,再利用△ABC的面积等于 +x+y=1,由此得到点(x,y)的轨迹.
+x+y=1,由此得到点(x,y)的轨迹.
解答:∵ ,∴
,∴ •(
•( )=2
)=2 ,即
,即  =2
=2 .
.
∴ cosA=
cosA= cos30°=2
cos30°=2 ,∴
,∴ =4,
=4,
故△ABC的面积等于 •sin30°=1.
•sin30°=1.
∵m、n、p分别表示△MBC、△MCA、△MAB的面积,由△ABC的面积为△MBC,△MCA,△MAB的面积之和1,
所以 +x+y=1,即 x+y=
+x+y=1,即 x+y= (x>0,y>0),
(x>0,y>0),
故选B.
点评:本题考查两个向量的数量积的定义,以及三角形的面积公式的应用,直线的一般式方程的特征,属于中档题.
分析:先求出|AB|•|AC|的值,再求出△ABC的面积等于1,再利用△ABC的面积等于
 +x+y=1,由此得到点(x,y)的轨迹.
+x+y=1,由此得到点(x,y)的轨迹.解答:∵
 ,∴
,∴ •(
•( )=2
)=2 ,即
,即  =2
=2 .
.∴
 cosA=
cosA= cos30°=2
cos30°=2 ,∴
,∴ =4,
=4,故△ABC的面积等于
 •sin30°=1.
•sin30°=1.∵m、n、p分别表示△MBC、△MCA、△MAB的面积,由△ABC的面积为△MBC,△MCA,△MAB的面积之和1,
所以
 +x+y=1,即 x+y=
+x+y=1,即 x+y= (x>0,y>0),
(x>0,y>0),故选B.
点评:本题考查两个向量的数量积的定义,以及三角形的面积公式的应用,直线的一般式方程的特征,属于中档题.

练习册系列答案
相关题目








 ,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若
,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若 ,则在平面直坐标系中点(x,y)的轨迹是( )
,则在平面直坐标系中点(x,y)的轨迹是( )


