题目内容
设数列{an}是首项为1公比为3的等比数列,把{an}中的每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N*,下列结论正确的是( )A.bn+1=3bn,且Sn=
 (3n-1)
(3n-1)B.bn+1=3bn-2,且Sn=
 (3n-1)
(3n-1)C.bn+1=3bn+4,且Sn=
 (3n-1)-2n
(3n-1)-2nD.bn+1=3bn-4,且Sn=
 (3n-1)-2n
(3n-1)-2n
【答案】分析:由题意知an=3n-1,bn=3n-1-2,bn+1=3bn+4.{bn}的前n项和Sn=(1-2)+(31-2)+(32-2)+(33-2)++(3n-1-2)=(1+31+32+33++3n-1)-2n=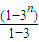 -2n=
-2n= (3n-1)-2n.
(3n-1)-2n.
解答:解:因为数列{an}是首项为1公比为3的等比数列,所以数列{an}的通项公式
an=3n-1,则依题意得,数列{bn}的通项公式为bn=3n-1-2,∴bn+1=3n-2,3bn=3(3n-1-2)=3n-6,
∴bn+1=3bn+4.{bn}的前n项和为:
Sn=(1-2)+(31-2)+(32-2)+(33-2)++(3n-1-2)=(1+31+32+33++3n-1)-2n=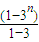 -2n
-2n
= (3n-1)-2n.
(3n-1)-2n.
故选C.
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.
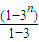 -2n=
-2n= (3n-1)-2n.
(3n-1)-2n.解答:解:因为数列{an}是首项为1公比为3的等比数列,所以数列{an}的通项公式
an=3n-1,则依题意得,数列{bn}的通项公式为bn=3n-1-2,∴bn+1=3n-2,3bn=3(3n-1-2)=3n-6,
∴bn+1=3bn+4.{bn}的前n项和为:
Sn=(1-2)+(31-2)+(32-2)+(33-2)++(3n-1-2)=(1+31+32+33++3n-1)-2n=
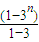 -2n
-2n=
 (3n-1)-2n.
(3n-1)-2n.故选C.
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列{an}是首项为1公比为3的等比数列,把{an}中的每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N*,下列结论正确的是( )
A、bn+1=3bn,且Sn=
| ||
B、bn+1=3bn-2,且Sn=
| ||
C、bn+1=3bn+4,且Sn=
| ||
D、bn+1=3bn-4,且Sn=
|