题目内容
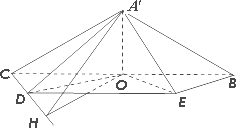
如图(1),在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=![]() ,O为BC的中点.将△ADE沿DE折起,得到如图(2)所示的四棱锥
,O为BC的中点.将△ADE沿DE折起,得到如图(2)所示的四棱锥![]() ,其中
,其中![]() .
.

(Ⅰ)证明:![]() 平面BCDE;
平面BCDE;
(Ⅱ)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
答案:
解析:
解析:
(Ⅰ)在图(1)中,易得![]()
连结![]() ,在
,在![]() 中,由余弦定理可得
中,由余弦定理可得
![]()
由翻折不变性可知![]() ,
,
所以![]() ,所以
,所以![]() ,
,
理可证![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.

(Ⅱ)传统法:过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
结合图1可知,![]() 为
为![]() 中点,故
中点,故![]() ,从而
,从而![]()
所以![]() ,所以二面角
,所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.
向量法:以O点为原点,建立空间直角坐标系O-xyz如图所示,
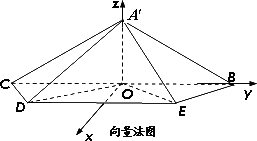
则![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则
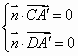 ,即
,即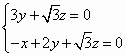 ,解得
,解得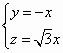 ,令
,令![]() ,得
,得![]()
由(Ⅰ)知,![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
所以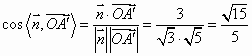 ,即二面角
,即二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

练习册系列答案
相关题目
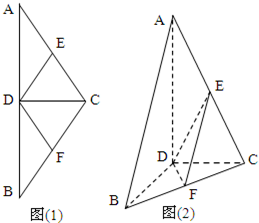 (2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))
(2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))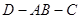 ,如图二,在二面角
,如图二,在二面角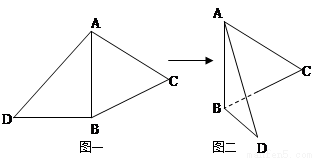
 中,
中,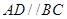 ,
,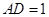 ,
,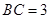 ,
,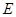 为
为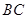 上一点,
上一点, 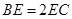 ,且
,且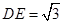 .将梯形
.将梯形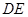 折成直二面角
折成直二面角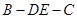 ,如图2所示.
,如图2所示.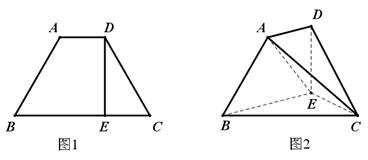
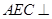 平面
平面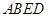 ;
;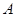 关于点
关于点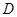 的对称点为
的对称点为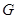 ,点
,点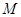 在
在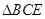 所在平面内,且直线
所在平面内,且直线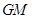 与平面
与平面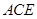 所成的角为
所成的角为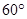 ,试求出点
,试求出点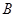 的最短距离.
的最短距离. 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点, ,现将
,现将

 DE?证明你的结论.
DE?证明你的结论. 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点, ,
, DE?证明你的结论.
DE?证明你的结论.