题目内容
(08年丰台区统一练习一理)(14分)
设函数![]() .
.
(Ⅰ)求f (x)的单调区间;
(Ⅱ)若当![]() 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;
(Ⅲ)若关于x的方程![]() 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
解析:(Ⅰ)函数的定义域为(-1, +∞).…………………………………………… 1分
∵ ![]() ,
,
由![]() ,得x>0;由
,得x>0;由![]() ,得
,得![]() .………………… 3分
.………………… 3分
∴ f (x)的递增区间是![]() ,递减区间是(-1, 0).………………… 4分
,递减区间是(-1, 0).………………… 4分
(Ⅱ)∵ 由![]() ,得x=0,x=-2(舍去)
,得x=0,x=-2(舍去)
由(Ⅰ)知f (x)在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
高三数学(理科)答案第3页(共6页)
又 ![]() ,
, ![]() , 且
, 且![]() .
.
∴ 当![]() 时,f (x)的最大值为
时,f (x)的最大值为![]() .
.
故当![]() 时,不等式f (x)<m恒成立.……………………………… 9分
时,不等式f (x)<m恒成立.……………………………… 9分
(Ⅲ)方程![]() ,
, ![]() .
.
记![]() ,
,
∵ ![]() ,
,
由![]() ,得x>1或x<-1(舍去). 由
,得x>1或x<-1(舍去). 由![]() , 得
, 得![]() .
.
∴ g(x)在[0,1]上递减, 在[1,2]上递增.
为使方程![]() 在区间[0, 2]上恰好有两个相异的实根,
在区间[0, 2]上恰好有两个相异的实根,
只须g(x)=0在[0,1]和![]() 上各有一个实数根,于是有
上各有一个实数根,于是有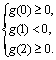
∵ ![]() ,
,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目