题目内容
设函数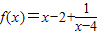 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).(1)求g(x)的表达式;
(2)解不等式
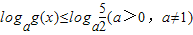 .
.
【答案】分析:(1)设出函数图象上的任意点的坐标,利用对称性求出对称点的坐标,代入已知方程,即可求出所求对称的函数的解析式.
(2)直接转化不等式,通过a的范围讨论大于1与a大于0小于1时,不等式的等价形式,然后求解即可.
解答:解:(1)设函数y=g(x)的图象上任意一点为(x,y),
则关于A(2,1)的对称点为(4-x,2-y),
又(4-x,2-y)在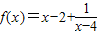 的图象上,
的图象上,
所以,2-y=(4-x)-2+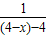 =x+
=x+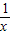 ,
,
即g(x) 的表达式为g(x)=x+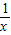 ,(x≠0).
,(x≠0).
(2)原不等式化为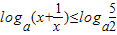 ,
,
当1<a时,有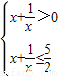 ,
,
解得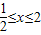 ,
,
当0<a<1时,有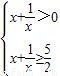 ,解得
,解得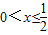 或x>2,
或x>2,
综上当a>1时,不等式的解集为{x|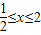 },
},
当0<a<1时,不等式的解集为{x|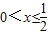 或x>2}.
或x>2}.
点评:本题考查函数的图象的对称性,函数的解析式的求法,对数不等式的解法,分类讨论思想的应用,考查计算能力.
(2)直接转化不等式,通过a的范围讨论大于1与a大于0小于1时,不等式的等价形式,然后求解即可.
解答:解:(1)设函数y=g(x)的图象上任意一点为(x,y),
则关于A(2,1)的对称点为(4-x,2-y),
又(4-x,2-y)在
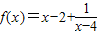 的图象上,
的图象上,所以,2-y=(4-x)-2+
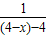 =x+
=x+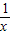 ,
,即g(x) 的表达式为g(x)=x+
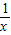 ,(x≠0).
,(x≠0).(2)原不等式化为
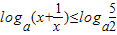 ,
,当1<a时,有
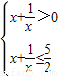 ,
,解得
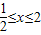 ,
,当0<a<1时,有
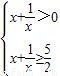 ,解得
,解得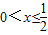 或x>2,
或x>2,综上当a>1时,不等式的解集为{x|
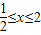 },
},当0<a<1时,不等式的解集为{x|
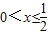 或x>2}.
或x>2}.点评:本题考查函数的图象的对称性,函数的解析式的求法,对数不等式的解法,分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
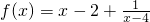 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).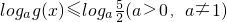 .
. 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x). .
.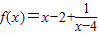 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).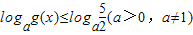 .
.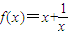 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).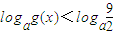 .
.