题目内容
下列给出的函数中,既不是奇函数也不是偶函数的是
A. |
B.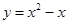 |
C. |
D. |
B
解析本题利用直接法解决,即根据判断函数奇偶性的一般步骤:如果定义域不关于原点对称,那么f(x)是非奇非偶函数,当定义域关于原点对称时,求出 f(-x)与-f(x)判断f(-x)=f(x),f(-x)=-f(x)是否成立,如果满足 f(-x)=-f(x),那么 f(x)就是奇函数.如果满足 f(-x)=f(x),那么 f(x)就是偶函数.如果都不满足,那么f(x)是非奇非偶函数.一一进行判定即可.
解:由题意知:A,B,C,D定义域都关于原点对称
A中满足∵y=2|x|
∴f(-x)=2|x|
∴f(-x)=f(x)
∴f(x)是偶函数.
B∵y=x2-x
∴f(-x)=(-x)2-(-x)=x2+x
-f(x)=-(x2-x)
∴f(x)≠f(-x),f(-x)≠-f(x)
故不是奇函数也不是偶函数
C∵y=2x
∴f(-x)=-2x,-f(x)=-2x
∴f(-x)=-f(x)
∴f(x)是奇函数
D∵y=x3
∴f(-x)=(-x)3,-f(x)=-x3
∴f(-x)=-f(x),
∴f(x)是奇函数
故选B

练习册系列答案
相关题目
下列函数在定义域内是奇函数的是
A.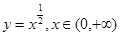 | B.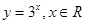 | C.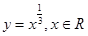 | D.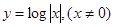 |
设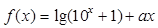 是偶函数,
是偶函数,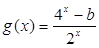 是奇函数,那么
是奇函数,那么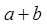 的值为( )
的值为( )
| A.1 | B.-1 | C.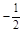 | D. |
已知函数f(x)=ax2-2ax+1(a>1),若x1<x2,且x1+x2=1+a,则( )
| A.f(x1)>f(x2) |
| B.f(x1)<f(x2) |
| C.f(x1)=f(x2) |
| D.f(x1)与f(x2)的大小不能确定 |
函数y=x2-2x的定义域为{0,1,2,3},那么其值域为( )
| A.{-1,0,3} | B.{0,1,2,3} |
| C.{y|-1≤y≤3} | D.{y|0≤y≤3} |
已知函数f(x)=若f(a)=,则a=
( )
| A.-1 | B. |
| C.-1或 | D.1或- |
一元二次方程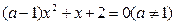 有两个异号实根的一个充分不必要条件是 ( )
有两个异号实根的一个充分不必要条件是 ( )
A.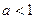 | B.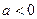 |
C.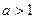 | D.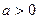 |
函数 的零点所在区间
的零点所在区间
A.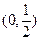 | B. | C.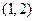 | D. |
 与指数函数
与指数函数 的图像只可能是
的图像只可能是