题目内容
如图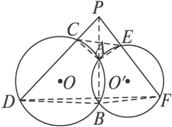
图
证明:连结AC、AE、CE、BD、BF、DF.
∵ABDC内接于⊙O,
∴∠PCA=∠PBD.
又∠CPB是公共角,
∴△PAC∽△PDB.
∴
.
∴PC·PD=PA·PB.
同理,PE·PF=PA·PB.
∴PC·PD=PE·PF.
∴
.
又∠CPE是公共角,
∴△PCE∽△PFD.
∴∠PCE=∠PFD.
∴C、D、F、E四点共圆.
练习册系列答案
相关题目
题目内容
如图
图
证明:连结AC、AE、CE、BD、BF、DF.
∵ABDC内接于⊙O,
∴∠PCA=∠PBD.
又∠CPB是公共角,
∴△PAC∽△PDB.
∴.
∴PC·PD=PA·PB.
同理,PE·PF=PA·PB.
∴PC·PD=PE·PF.
∴.
又∠CPE是公共角,
∴△PCE∽△PFD.
∴∠PCE=∠PFD.
∴C、D、F、E四点共圆.
等于( )
+
B.-
D.
+
=a，
=b，
=c，则
等于（ ）
