题目内容
记数列{an}的前n项和为Sn,所有奇数项之和为S′,所有偶数项之和为S″.(1)若{an}是等差数列,项数n为偶数,首项a1=1,公差
 ,且S″-S′=15,求Sn;
,且S″-S′=15,求Sn;(2)若无穷数列{an}满足条件:①
 (n∈N*),②S′=S″.求{an}的通项;
(n∈N*),②S′=S″.求{an}的通项;(3)若{an}是等差数列,首项a1>0,公差d∈N*,且S′=36,S″=27,请写出所有满足条件的数列.
【答案】分析:(1)因为{an}是等差数列且项数n为偶数,所以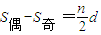 ,根据公式可以求出n,从而求出Sn;(2)先把递推公式
,根据公式可以求出n,从而求出Sn;(2)先把递推公式 ,往后递推一项得
,往后递推一项得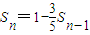 ,然后两式相减可以推出数列{an}是从第二项开始的无穷等比数列,公比
,然后两式相减可以推出数列{an}是从第二项开始的无穷等比数列,公比 ,且0<|q|<1,然后根据无穷等比数列所有项和公式
,且0<|q|<1,然后根据无穷等比数列所有项和公式 ,求出{an}的通项;(3)先判断出数列的项数为奇数,然后写出奇数项的和与偶数项的和进行作差或者作商,求出公差的取值范围d<3.又d∈N*,所以,d=1或d=2 从而确定所求数列.
,求出{an}的通项;(3)先判断出数列的项数为奇数,然后写出奇数项的和与偶数项的和进行作差或者作商,求出公差的取值范围d<3.又d∈N*,所以,d=1或d=2 从而确定所求数列.
解答:解:由题意知
(1)若数列{an}项数n为偶数,由已知,得S″-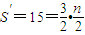
解得n=20,
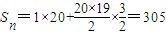 ;
;
(2)∵ (n∈N*)①
(n∈N*)①
∴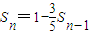 (n∈N*,n≥2)②
(n∈N*,n≥2)②
即①减去②得: .
.
所以数列{an}是从第二项开始的无穷等比数列,公比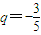 ,且0<|q|<1
,且0<|q|<1
∴ ,
,
 ,
,
又∵S′=S″,
∴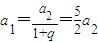 ,
,
又∵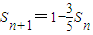 (n∈N*),
(n∈N*),
当n=1时,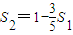
∴8a1+5a2=5
∴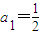
所以,对应的数列的通项为
(3)假设数列{an}项数n为偶数,S″-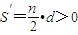 与S″-S′=-9矛盾.
与S″-S′=-9矛盾.
故数列{an}项数n不为偶数.
解法1:设数列{an}项数n=2k+1(k∈N),
则
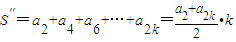
∵a1+a2k+1=a2+a2k,
∴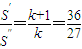 ,
,
解得k=3,项数n=2×3+1=7,
∵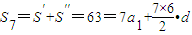 ,
,
∴a1+3d=9,
∵a1=9-3d>0,
∴d<3.又d∈N*,所以,d=1或d=2.
当d=1时,a1=6,此时,an=6+(n-1)•1=n+5,
所以,该数列为:6,7,8,9,10,11,12.
当d=2时,a1=3,此时,an=3+(n-1)•2=2n+1
所以,该数列为:3,5,7,9,11,13,15.
解法2:
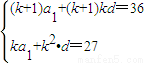 ,
,
解得k=3,项数n=2×3+1=7,
∵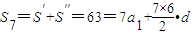 ,
,
∴a1+3d=9,∵a1=9-3d>0,
∴d<3.又d∈N*,所以,d=1或d=2.
当d=1时,a1=6,此时,an=6+(n-1)•1=n+5,
所以,该数列为:6,7,8,9,10,11,12.
当d=2时,a1=3,此时,an=3+(n-1)•2=2n+1
所以,该数列为:3,5,7,9,11,13,15.
点评:本题主要考查等差数列的奇数项的和S′与偶数项的和S∥的公式,以及无穷等比数列的所有项和的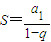 ,对学生的能力要求比较高,有一定的难度.
,对学生的能力要求比较高,有一定的难度.
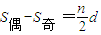 ,根据公式可以求出n,从而求出Sn;(2)先把递推公式
,根据公式可以求出n,从而求出Sn;(2)先把递推公式 ,往后递推一项得
,往后递推一项得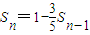 ,然后两式相减可以推出数列{an}是从第二项开始的无穷等比数列,公比
,然后两式相减可以推出数列{an}是从第二项开始的无穷等比数列,公比 ,且0<|q|<1,然后根据无穷等比数列所有项和公式
,且0<|q|<1,然后根据无穷等比数列所有项和公式 ,求出{an}的通项;(3)先判断出数列的项数为奇数,然后写出奇数项的和与偶数项的和进行作差或者作商,求出公差的取值范围d<3.又d∈N*,所以,d=1或d=2 从而确定所求数列.
,求出{an}的通项;(3)先判断出数列的项数为奇数,然后写出奇数项的和与偶数项的和进行作差或者作商,求出公差的取值范围d<3.又d∈N*,所以,d=1或d=2 从而确定所求数列.解答:解:由题意知
(1)若数列{an}项数n为偶数,由已知,得S″-
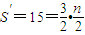
解得n=20,
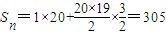 ;
;(2)∵
 (n∈N*)①
(n∈N*)①∴
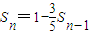 (n∈N*,n≥2)②
(n∈N*,n≥2)②即①减去②得:
 .
. 所以数列{an}是从第二项开始的无穷等比数列,公比
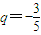 ,且0<|q|<1
,且0<|q|<1∴
 ,
, ,
,又∵S′=S″,
∴
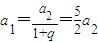 ,
,又∵
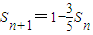 (n∈N*),
(n∈N*),当n=1时,
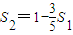
∴8a1+5a2=5
∴
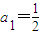
所以,对应的数列的通项为

(3)假设数列{an}项数n为偶数,S″-
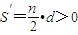 与S″-S′=-9矛盾.
与S″-S′=-9矛盾.故数列{an}项数n不为偶数.
解法1:设数列{an}项数n=2k+1(k∈N),
则

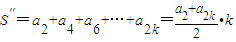
∵a1+a2k+1=a2+a2k,
∴
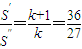 ,
,解得k=3,项数n=2×3+1=7,
∵
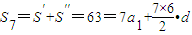 ,
,∴a1+3d=9,
∵a1=9-3d>0,
∴d<3.又d∈N*,所以,d=1或d=2.
当d=1时,a1=6,此时,an=6+(n-1)•1=n+5,
所以,该数列为:6,7,8,9,10,11,12.
当d=2时,a1=3,此时,an=3+(n-1)•2=2n+1
所以,该数列为:3,5,7,9,11,13,15.
解法2:

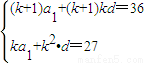 ,
,解得k=3,项数n=2×3+1=7,
∵
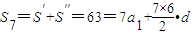 ,
,∴a1+3d=9,∵a1=9-3d>0,
∴d<3.又d∈N*,所以,d=1或d=2.
当d=1时,a1=6,此时,an=6+(n-1)•1=n+5,
所以,该数列为:6,7,8,9,10,11,12.
当d=2时,a1=3,此时,an=3+(n-1)•2=2n+1
所以,该数列为:3,5,7,9,11,13,15.
点评:本题主要考查等差数列的奇数项的和S′与偶数项的和S∥的公式,以及无穷等比数列的所有项和的
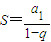 ,对学生的能力要求比较高,有一定的难度.
,对学生的能力要求比较高,有一定的难度. 
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
记数列{an}的前n项和为Sn,且Sn=2n(n-1),则该数列是( )
| A、公比为2的等比数列 | ||
B、公比为
| ||
| C、公差为2的等差数列 | ||
| D、公差为4的等差数列 |