题目内容
9.设函数f(x)=$\left\{{{\;}_{-2-\sqrt{x-4},x≥1}^{{{({x+1})}^2},x<1}}$,则f[f(5)]=( )| A. | -3 | B. | 4 | C. | 9 | D. | 16 |
分析 直接利用分段函数,由里及外逐步求解函数值即可.
解答 解:函数f(x)=$\left\{{{\;}_{-2-\sqrt{x-4},x≥1}^{{{({x+1})}^2},x<1}}$,则f(5)=-2-$\sqrt{5-4}$=-3.
f[f(5)]=f(-3)=(-3+1)2=4.
故选:B.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
19.已知f(x)=$\left\{\begin{array}{l}{2x+1,x∈[-2,2]}\\{1+{x}^{2},x∈(2,4]}\end{array}\right.$,若${∫}_{k}^{3}$f(x)dx=$\frac{40}{3}$,则k的值为( )
| A. | 0 | B. | 0或-1 | C. | 0或1 | D. | -1 |
14.如图是某个闭合电路的一部分,每个元件正常工作的概率为$\frac{1}{2}$,则从A到B这部分电路能正常工作的概率为( )
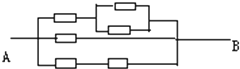

| A. | $\frac{27}{32}$ | B. | $\frac{55}{64}$ | C. | $\frac{115}{128}$ | D. | $\frac{49}{64}$ |
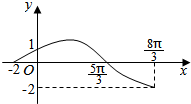 已知函数y=$\left\{\begin{array}{l}{kx+1(-2≤x<0)}\\{2sin(wx+φ)(0≤x≤\frac{8π}{3})}\end{array}\right.$的图象如图所示,试求k,ω,φ的值.
已知函数y=$\left\{\begin{array}{l}{kx+1(-2≤x<0)}\\{2sin(wx+φ)(0≤x≤\frac{8π}{3})}\end{array}\right.$的图象如图所示,试求k,ω,φ的值.