题目内容
已知复数z=a2-7a+6+(a2-5a-6)i(a∈R),去a分别为何值时,(1)z是实数;
(2)z是纯虚数;
(3)当|
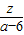 |=
|=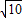 时,求z的共轭复数.
时,求z的共轭复数.
【答案】分析:(1)由复数定义可得a2-5a-6=0,即可;
(2)由纯虚数定义可得a2-7a+6=0,且a2-5a-6≠0,解出即可;
(3)由条件可得,|(a-1)+(a+1)i|=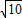 ,由模定义可得(a-1)2+(a+1)2=10,解出a可得z,进而得
,由模定义可得(a-1)2+(a+1)2=10,解出a可得z,进而得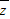 ;
;
解答:解:(1)由Z是实数,则a2-5a-6=0,得a=6或a=-1;
(2)由Z是纯虚数,则a2-7a+6=0,且a2-5a-6≠0,得a=1;
(3)当|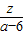 |=
|=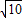 时,|(a-1)+(a+1)i|=
时,|(a-1)+(a+1)i|=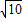 ,
,
得(a-1)2+(a+1)2=10,得a=±2;
当a=2时,z=-4-12i,得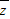 =-4+12i;
=-4+12i;
当a=-2时,z=24+8i,得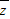 =24-8i.
=24-8i.
点评:本题考查复数的基本概念、复数求模,属基础题.
(2)由纯虚数定义可得a2-7a+6=0,且a2-5a-6≠0,解出即可;
(3)由条件可得,|(a-1)+(a+1)i|=
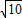 ,由模定义可得(a-1)2+(a+1)2=10,解出a可得z,进而得
,由模定义可得(a-1)2+(a+1)2=10,解出a可得z,进而得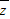 ;
;解答:解:(1)由Z是实数,则a2-5a-6=0,得a=6或a=-1;
(2)由Z是纯虚数,则a2-7a+6=0,且a2-5a-6≠0,得a=1;
(3)当|
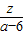 |=
|=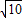 时,|(a-1)+(a+1)i|=
时,|(a-1)+(a+1)i|=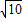 ,
,得(a-1)2+(a+1)2=10,得a=±2;
当a=2时,z=-4-12i,得
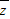 =-4+12i;
=-4+12i;当a=-2时,z=24+8i,得
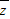 =24-8i.
=24-8i.点评:本题考查复数的基本概念、复数求模,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目