题目内容
如果直线(2a+5)x+(a-2)y+4=0与直线(2-a)x+(a+3)y-1=0互相垂直,则a的值等于( )
| A.2 | B.-2 | C.2,-2 | D.2,0,-2 |
C
解:设直线(2a+5)x+(a-2)y+4=0为直线M; 直线(2-a)x+(a+3)y-1=0为直线N
1. 当直线M斜率不存在时,即直线M的倾斜角为90°,即a-2="0," a=2时,直线N的斜率为0,即直线M的倾斜角为0°。 故:直线M与直线N互相垂直,所以a=2时两直线互相垂直
2.当直线M和N的斜率都存在时,Km="(2a+5)/(a-2)" , Kn="(2-a)/(a+3)" 要使两直线互相垂直,即让两直线的斜率相乘为-1。 故:a=-2
3.当直线N斜率不存在时,显然两直线不垂直。
综上所述:a=2或a=-2
故选C。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的射影是
上的射影是 ,则直线
,则直线



 与
与 平行,则
平行,则 的值等于( )
的值等于( )
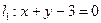 与直线
与直线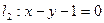 的交点M,且分别满足下列条件的直线方程:
的交点M,且分别满足下列条件的直线方程: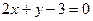 平行;
平行; 



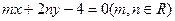 将圆
将圆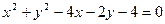 分成两段相等的弧,则m+n等于 ( )
分成两段相等的弧,则m+n等于 ( )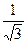 x的倾斜角的2倍,则该直线的方程为 。
x的倾斜角的2倍,则该直线的方程为 。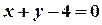 上,那么x2+y2的最小值是( )
上,那么x2+y2的最小值是( )