题目内容
已知函数f(x)=x2,g(x)=|x-2|.(1)解不等式f(x)>g(x);
(2)设函数f(x)的图象为C1,g(x)的图象为C2,l是和曲线C1相切且与曲线C2无公共点的直线,求直线l的斜率的取值范围.
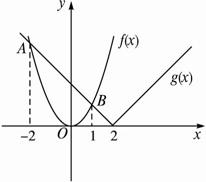
解法一:(1)∵f(x)=x2,g(x)=|x-2|,在同一直角坐标系中画出函数f(x)和g(x)的图象,
?
解方程组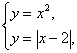 得A(-2,4),B(1,1), ?
得A(-2,4),B(1,1), ?
∴不等式f(x)>g(x)的解集为函数f(x)的图象C1位于函数g(x)的图象C2的上方时,自变量x的取值范围,即为{x|x<-2或x>1}.?
综上可得,原不等式的解集为{x|x<-2或x>1}.
 ?
?
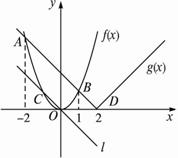
(2)如图所示,设直线l为曲线C1的切线,切点为C.当切线l的斜率为-1时,切线l与曲线C2
无公共点, ?
此时,若让切线l按逆时针方向沿曲线C1运动至坐标原点O时,切线l与曲线C2恰有一个公共点D,由此可得,当切线l的斜率k∈[-1,0)时,直线为l与曲线C2无公共点. ?
解法二:(1)∵f(x)=x2,g(x)=|x-2|,f(x)≥g(x),x2>|x-2|,??
当x≤2时,得x2>2-x,解得x<-2或1<x≤2; ?
当x>2时,得x2>x-2,解得x>2. ?
综上可得,原不等式的解集为{x|x<-2或x>1}. ?
(2)∵f′(x)=2x,直线l与曲线C1相切时的切点为M(x0,x02),则直线l的方程为y-x02=2x0
(x-x0),即y=2x0x-x02,又直线l与曲线C2无公共点,则需满足方程组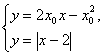 无解,
无解,
即方程2x0x-x02=|x-2|无解. ?
当x≥2时,方程2x0x-x02=|x-2|可化为2x0x-x02=x-2,即(2x0-1)x=x02-2, ①?
若x0=![]() ,方程①无解;?
,方程①无解;?
若x0≠![]() ,则方程①无解需满足不等式
,则方程①无解需满足不等式![]() <2,由此解得x0<0或
<2,由此解得x0<0或![]() <x0<4.?
<x0<4.?
∴方程①无解的条件是x0<0或![]() ≤x0<4.?
≤x0<4.?
当x<2时,方程2x0x-x02=|x-2|可化为2x0x-x02=2-x,即(2x0+1)x=x02+2, ②?
若x0=-![]() ,方程②无解;?
,方程②无解;?
若x0≠-![]() ,则方程②无解需满足不等式
,则方程②无解需满足不等式![]() ≥2,由此解得-
≥2,由此解得-![]() <x0≤0或x0≥4.?
<x0≤0或x0≥4.?
∴方程②无解的条件是-![]() ≤x0≤0或x0≥4.?
≤x0≤0或x0≥4.?
综上可得,方程2x0x-x02=|x-2|无解的条件是-![]() ≤x0<0.?
≤x0<0.?
故f′(x0)=2x0的取值范围是[-1,0),即直线l的斜率的取值范围是[-1,0).

 导学教程高中新课标系列答案
导学教程高中新课标系列答案