题目内容
(2012•泰安一模)已知数列{an}是等差数列,满足a2=5,a4=13.数列{bn}的前n项和是Tn,且Tn+bn=3.
(1)求数列{an}及数列{bn}的通项公式;
(II)若cn=an•bn,试比较cn与cn+1的大小.
(1)求数列{an}及数列{bn}的通项公式;
(II)若cn=an•bn,试比较cn与cn+1的大小.
分析:(Ι)由数列{an}为等差数列,根据a2=5,a4=13,利用等差数列的性质求出公差d的值,进而由a2及d的值,可得出等差数列{an}的通项公式,当n=1时,T1=b1,根据Tn+bn=3①,得到b1的值,再由数列的递推式得到Tn-Tn-1=bn,由Tn-1+bn-1=3,记作②,①-②得到bn=
bn-1,可确定出此数列为公比为
的等比数列,写出{bn}的通项公式即可;
(II)将第一问得到的数列{an}及数列{bn}的通项公式代入cn=an•bn,整理后,表示出cn-cn-1,令cn-cn-1=0,求出n的值,可得出cn-cn-1大于0及小于0时n的范围,进而得出n为1或2时,cn>cn-1;当n≥3时,cn<cn-1.
| 1 |
| 2 |
| 1 |
| 2 |
(II)将第一问得到的数列{an}及数列{bn}的通项公式代入cn=an•bn,整理后,表示出cn-cn-1,令cn-cn-1=0,求出n的值,可得出cn-cn-1大于0及小于0时n的范围,进而得出n为1或2时,cn>cn-1;当n≥3时,cn<cn-1.
解答:解:(Ι)∵数列{an}是等差数列,满足a2=5,a4=13,
∴公差d=
=4,
∴an=a2+(n-2)d=4n-3,
∵数列{bn}的前n项和是Tn,Tn+bn=3①,
∴当n=1时,T1=b1,即b1=
;
当n≥2时,Tn-Tn-1=bn,由题意可得Tn-1+bn-1=3②,
①-②得:2bn-bn-1=0,即bn=
bn-1,即公比q=
,
∴bn=
•(
)n-1;
(II)∵an=4n-3,bn=
•(
)n-1,
∴cn=an•bn=(4n-3)•
•(
)n-1=(6n-
)•(
)n-1,
令cn-cn+1=(6n-
)•(
)n-1-(6n+6-
)•(
)n=(
)n-1(6n-
-3n-3+
)=(
)n-1(3n-
)=0,
解得:n=
,
则n=2时,cn>cn+1;当n≥3时,cn<cn+1.
∴公差d=
| a4-a2 |
| 2 |
∴an=a2+(n-2)d=4n-3,
∵数列{bn}的前n项和是Tn,Tn+bn=3①,
∴当n=1时,T1=b1,即b1=
| 3 |
| 2 |
当n≥2时,Tn-Tn-1=bn,由题意可得Tn-1+bn-1=3②,
①-②得:2bn-bn-1=0,即bn=
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=
| 3 |
| 2 |
| 1 |
| 2 |
(II)∵an=4n-3,bn=
| 3 |
| 2 |
| 1 |
| 2 |
∴cn=an•bn=(4n-3)•
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
令cn-cn+1=(6n-
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 21 |
| 4 |
解得:n=
| 21 |
| 12 |
则n=2时,cn>cn+1;当n≥3时,cn<cn+1.
点评:此题考查了等差数列的性质,等比数列的确定,等差、等比数列的通项公式,以及作差法的运用,熟练掌握性质及公式是解本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
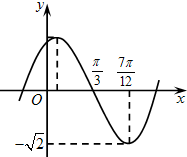 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则