题目内容
等比数列{an}中,其公比q<0,且a2=1-a1,a4=4-a3,则a4+a5等于( )
| A.8 | B.-8 | C.16 | D.-16 |
B
解析试题分析:由题意得 ,解得
,解得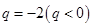 ,
,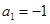 ,所以
,所以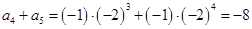 ,所以正确答案为B.
,所以正确答案为B.
考点:等比数列

练习册系列答案
相关题目
已知等比数列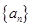 ,它的前
,它的前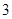 项为
项为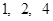 ,前
,前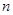 项和为
项和为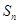 ,则使得
,则使得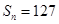 的
的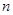 的值是( )
的值是( )
A.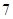 | B.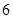 | C.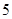 | D.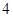 |
设等比数列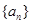 的公比
的公比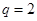 ,前
,前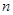 项和为
项和为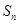 ,则
,则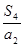 的值为( )
的值为( )
A.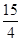 | B.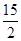 | C.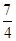 | D.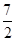 |
等比数列 共有奇数项,所有奇数项和
共有奇数项,所有奇数项和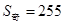 ,所有偶数项和
,所有偶数项和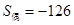 ,末项是
,末项是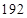 ,则首项
,则首项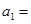 ( )
( )
A. | B. | C. | D. |
等比数列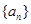 中,已知对任意正整数
中,已知对任意正整数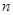 ,
,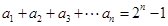 ,则
,则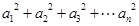 等于( )
等于( )
A.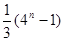 | B.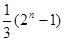 | C.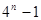 | D.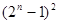 |
已知数列{an},如果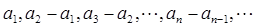 是首项为1公比为2的等比数列,那么an=( )
是首项为1公比为2的等比数列,那么an=( )
| A.2n+1-1 | B.2n-1 | C.2n-1 | D.2n +1 |
等比数列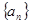 中,
中, 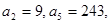 则
则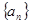 的前4项和为( )
的前4项和为( )
| A.81 | B.120 | C.168 | D.192 |
已知a1,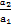 ,
,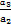 ,…,
,…,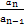 ,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
| A.25050 | B.24950 | C.2100 | D.299 |
已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=( ).
| A.2n-1 | B.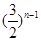 | C.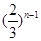 | D.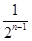 |