题目内容
在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的 倍后得到点
倍后得到点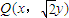 ,且满足
,且满足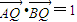 .
.(I)求动点P所在曲线C的方程;
(II)过点B作斜率为
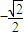 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且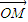 +
+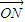 +
+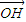 =
=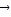 ,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
【答案】分析:(I)确定向量AQ,BQ的坐标,利用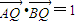 ,即可得到动点P所在曲线C的轨迹方程.
,即可得到动点P所在曲线C的轨迹方程.
(II)假设l的方程与椭圆方程联立,利用向量知识,确定M,N,G,H的坐标,进而确定点到四点的距离相等,从而可得结论.
解答:解::(I)依据题意,有 =(x+1,
=(x+1,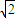 y),
y),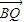 =(x-1,
=(x-1,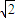 y),
y),
∵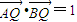 ,∴x2-1+2y2=1,
,∴x2-1+2y2=1,
∴动点P所在曲线C的轨迹方程是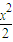 +y2=1.
+y2=1.
(II)因直线l过点B,且斜率为k=-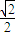 ,故有l:y=-
,故有l:y=-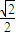 (x-1).
(x-1).
联立方程组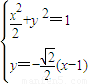 ,得2x2-2x-1=0.
,得2x2-2x-1=0.
设两曲线的交点为M(x1,y1)、N(x2,y2),∴x1+x2=1,y1+y2=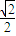 .
.
又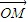 +
+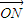 +
+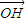 =
=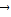 ,点G与点H关于原点对称,于是,可得点H(-1,-
,点G与点H关于原点对称,于是,可得点H(-1,-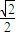 )、G(1,
)、G(1,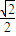 ).
).
若线段MN、GH的中垂线分别为l1和l2,则有l1:y-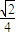 =
=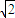 (x-
(x- ),l2:y=-
),l2:y=-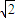 x.
x.
联立方程组,解得l1和l2的交点为O1( ,-
,-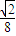 ).
).
因此,可算得|O1H|=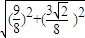 =
= ,|O1M|=
,|O1M|=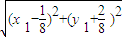 =
=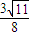 .
.
所以,四点M、G、N、H共圆,圆心坐标为O1( ,-
,-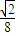 ),半径为
),半径为 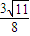 .
.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查四点共圆,正确运用向量知识,确定圆心坐标与半径是关键,属于难题.
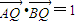 ,即可得到动点P所在曲线C的轨迹方程.
,即可得到动点P所在曲线C的轨迹方程.(II)假设l的方程与椭圆方程联立,利用向量知识,确定M,N,G,H的坐标,进而确定点到四点的距离相等,从而可得结论.
解答:解::(I)依据题意,有
 =(x+1,
=(x+1,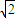 y),
y),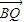 =(x-1,
=(x-1,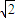 y),
y),∵
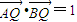 ,∴x2-1+2y2=1,
,∴x2-1+2y2=1,∴动点P所在曲线C的轨迹方程是
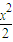 +y2=1.
+y2=1.(II)因直线l过点B,且斜率为k=-
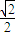 ,故有l:y=-
,故有l:y=-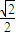 (x-1).
(x-1).联立方程组
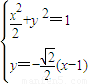 ,得2x2-2x-1=0.
,得2x2-2x-1=0.设两曲线的交点为M(x1,y1)、N(x2,y2),∴x1+x2=1,y1+y2=
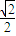 .
.又
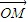 +
+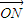 +
+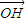 =
=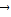 ,点G与点H关于原点对称,于是,可得点H(-1,-
,点G与点H关于原点对称,于是,可得点H(-1,-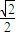 )、G(1,
)、G(1,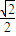 ).
).若线段MN、GH的中垂线分别为l1和l2,则有l1:y-
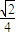 =
=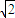 (x-
(x- ),l2:y=-
),l2:y=-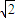 x.
x.联立方程组,解得l1和l2的交点为O1(
 ,-
,-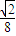 ).
).因此,可算得|O1H|=
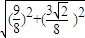 =
= ,|O1M|=
,|O1M|=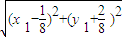 =
=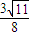 .
.所以,四点M、G、N、H共圆,圆心坐标为O1(
 ,-
,-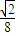 ),半径为
),半径为 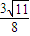 .
.点评:本题考查椭圆的标准方程,考查向量知识的运用,考查四点共圆,正确运用向量知识,确定圆心坐标与半径是关键,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
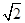 倍后得到点Q(x,
倍后得到点Q(x,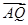 ·
· =1.
=1.  的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且 +
+ +
+ =
=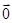 ,试求△MNH的面积.
,试求△MNH的面积. 倍后得到点Q(x,
倍后得到点Q(x, ·
· =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且 +
+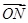 +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积. 倍后得到点Q(x,
倍后得到点Q(x, y),且满足
y),且满足 •
• =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且 +
+ +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积.