题目内容
在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的 倍后得到点Q(x,
倍后得到点Q(x, y),且满足
y),且满足 •
• =1.
=1.(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)过点B作斜率为-
 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且 +
+ +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积.
【答案】分析:(Ⅰ)设点P的坐标为(x,y),则点Q的坐标为(x, y),表示出
y),表示出 =(x+1,
=(x+1, y),
y), =(x-1,
=(x-1, y),利用
y),利用 •
• =1,即可求得动点P所在曲线C的方程;
=1,即可求得动点P所在曲线C的方程;
(Ⅱ)设出l:y=- (x-1),与椭圆联立方程组
(x-1),与椭圆联立方程组 ,消去y,得2x2-2x-1=0,利用
,消去y,得2x2-2x-1=0,利用 +
+ +
+ =
= ,确定H的坐标,计算|MN|,及H到直线l的距离即可求出△MNH的面积.
,确定H的坐标,计算|MN|,及H到直线l的距离即可求出△MNH的面积.
解答:解:(Ⅰ)设点P的坐标为(x,y),则点Q的坐标为(x, y).
y).
依据题意,有 =(x+1,
=(x+1, y),
y),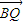 =(x-1,
=(x-1, y).…(2分)
y).…(2分)
∵ •
• =1,
=1,
∴x2-1+2y2=1.
∴动点P所在曲线C的方程是 +y2=1 …(4分)
+y2=1 …(4分)
(Ⅱ)因直线l过点B,且斜率为k=- ,故有l:y=-
,故有l:y=-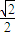 (x-1)…(5分)
(x-1)…(5分)
联立方程组 ,消去y,得2x2-2x-1=0.…(7分)
,消去y,得2x2-2x-1=0.…(7分)
设M(x1,y1)、N(x2,y2),可得 ,于是
,于是 .…(8分)
.…(8分)
又 +
+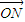 +
+ =
= ,得
,得 =(-x1-x2,-y1-y2),即H(-1,-
=(-x1-x2,-y1-y2),即H(-1,- )…(10分)
)…(10分)
∴|MN|= ,…(12分)
,…(12分)
又l: x+2y-
x+2y- =0,则H到直线l的距离为d=
=0,则H到直线l的距离为d=
故所求△MNH的面积为S= .…(14分)
.…(14分)
点评:本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查三角形面积的计算,计算弦长及点到直线的距离是关键.
 y),表示出
y),表示出 =(x+1,
=(x+1, y),
y), =(x-1,
=(x-1, y),利用
y),利用 •
• =1,即可求得动点P所在曲线C的方程;
=1,即可求得动点P所在曲线C的方程;(Ⅱ)设出l:y=-
 (x-1),与椭圆联立方程组
(x-1),与椭圆联立方程组 ,消去y,得2x2-2x-1=0,利用
,消去y,得2x2-2x-1=0,利用 +
+ +
+ =
= ,确定H的坐标,计算|MN|,及H到直线l的距离即可求出△MNH的面积.
,确定H的坐标,计算|MN|,及H到直线l的距离即可求出△MNH的面积.解答:解:(Ⅰ)设点P的坐标为(x,y),则点Q的坐标为(x,
 y).
y).依据题意,有
 =(x+1,
=(x+1, y),
y),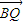 =(x-1,
=(x-1, y).…(2分)
y).…(2分)∵
 •
• =1,
=1,∴x2-1+2y2=1.
∴动点P所在曲线C的方程是
 +y2=1 …(4分)
+y2=1 …(4分)(Ⅱ)因直线l过点B,且斜率为k=-
 ,故有l:y=-
,故有l:y=-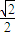 (x-1)…(5分)
(x-1)…(5分)联立方程组
 ,消去y,得2x2-2x-1=0.…(7分)
,消去y,得2x2-2x-1=0.…(7分)设M(x1,y1)、N(x2,y2),可得
 ,于是
,于是 .…(8分)
.…(8分)又
 +
+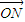 +
+ =
= ,得
,得 =(-x1-x2,-y1-y2),即H(-1,-
=(-x1-x2,-y1-y2),即H(-1,- )…(10分)
)…(10分)∴|MN|=
 ,…(12分)
,…(12分)又l:
 x+2y-
x+2y- =0,则H到直线l的距离为d=
=0,则H到直线l的距离为d=
故所求△MNH的面积为S=
 .…(14分)
.…(14分)点评:本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查三角形面积的计算,计算弦长及点到直线的距离是关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
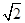 倍后得到点Q(x,
倍后得到点Q(x,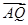 ·
· =1.
=1.  的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且 +
+ +
+ =
=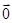 ,试求△MNH的面积.
,试求△MNH的面积. 倍后得到点Q(x,
倍后得到点Q(x, ·
· =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且 +
+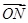 +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积.