题目内容
由以下条件分别给出数列{an}:
(1){3 an}是等比数列;(2)前n项和Sn=n2+2;
(3)a1>0,且ak=
(a1+a2+…+ak-1)(k≥2);(4)2an+1=an+an-1(n≥2);
以上能使{an}成等差数列的条件的序号是
(1){3 an}是等比数列;(2)前n项和Sn=n2+2;
(3)a1>0,且ak=
| 2 | k-1 |
以上能使{an}成等差数列的条件的序号是
(1),(3)
(1),(3)
.分析:根据题意,依次分析所给的条件,对于(1),若{3 an}是等比数列,设其公比为q,利用等比数列的定义可得an-an-1=log3q,则数列{an}为等差数列;对于(2),由其前n项和Sn=n2+2,求出数列{an}的前3项,即可得数列{an}不是等差数列;对于(3),对ak=
(a1+a2+…+ak-1)变形可得(k-1)ak=2Sk-1①,进而可得,(k-2)ak-1=2Sk-2②,①-②可得,(k-1)ak=kak-1,分析可得其符合等差数列的定义,则数列{an}为等差数列;对于(4),由2an+1=an+an-1可得an+1-an=an-1-an+1,分析可得其不符合等差数列的定义,则数列{an}不是等差数列;
| 2 |
| k-1 |
解答:解:根据题意,
对于(1),若{3 an}是等比数列,设其公比为q,则有
=3an-an-1=q>0,则an-an-1=log3q,则数列{an}为等差数列;
对于(2),由其前n项和Sn=n2+2,可得a1=3,a2=S2-S1=3,a3=S3-S2=5,不符合等差数列的定义,则数列{an}不是等差数列;
对于(3),ak=
(a1+a2+…+ak-1)⇒(k-1)ak=2Sk-1①,令k-1=k可得,(k-2)ak-1=2Sk-2②,①-②整理可得,(k-1)ak=kak-1,即
=
,
设
=
=m,变形可得an-an-1=m,符合等差数列的定义,则数列{an}为等差数列;
对于(4),由2an+1=an+an-1可得an+1-an=an-1-an+1,不符合等差数列的定义,则数列{an}不是等差数列;
故答案为(1)(3).
对于(1),若{3 an}是等比数列,设其公比为q,则有
| 3an |
| 3an-1 |
对于(2),由其前n项和Sn=n2+2,可得a1=3,a2=S2-S1=3,a3=S3-S2=5,不符合等差数列的定义,则数列{an}不是等差数列;
对于(3),ak=
| 2 |
| k-1 |
| ak |
| k |
| ak-1 |
| k-1 |
设
| ak |
| k |
| ak-1 |
| k-1 |
对于(4),由2an+1=an+an-1可得an+1-an=an-1-an+1,不符合等差数列的定义,则数列{an}不是等差数列;
故答案为(1)(3).
点评:本题考查等差数列的确定,常见的方法有定义法、通项公式发、等差中项法等.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目

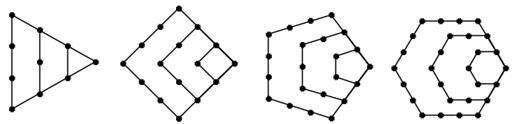
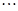 ,将构图边数增加到
,将构图边数增加到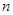 可得到“
可得到“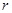 项为
项为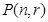 ,
,
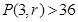 的最小
的最小