题目内容
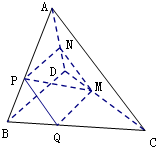
如图在四面体ABCD中，若截面PQMN是正方形，则在下列命题中正确的有______．（填上所有正确命题的序号）
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°．
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°．
在四面体ABCD中，∵截面PQMN是正方形，∴PQ∥MN，PQ?平面ACD，MN?平面ACD，∴PQ∥平面ACD．
∵平面ACB∩平面ACD=AC，∴PQ∥AC，可得AC∥平面PQMN．
同理可得BD∥平面PQMN，BD∥PN．
∵PN⊥PQ，∴AC⊥BD．
由BD∥PN，
∴∠MPN是异面直线PM与BD所成的角，且为45°．
由上面可知：BD∥PN，PQ∥AC．
∴
=
，
=
，
而AN≠DN，PN=MN，
∴BD≠AC．
综上可知：①③④都正确．
故答案为：①③④．
∵平面ACB∩平面ACD=AC，∴PQ∥AC，可得AC∥平面PQMN．
同理可得BD∥平面PQMN，BD∥PN．
∵PN⊥PQ，∴AC⊥BD．
由BD∥PN，
∴∠MPN是异面直线PM与BD所成的角，且为45°．
由上面可知：BD∥PN，PQ∥AC．
∴
| PN |
| BD |
| AN |
| AD |
| MN |
| AC |
| DN |
| AD |
而AN≠DN，PN=MN，
∴BD≠AC．
综上可知：①③④都正确．
故答案为：①③④．
练习册系列答案
相关题目
