题目内容
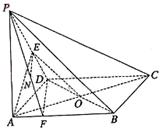
(本小题満分12分) 如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.

【答案】
P(0,0,2)、E(0,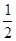 ,1),
,1),
(Ⅰ)建立如图所示的空间直角坐标系,
则A、B、C、D、P、E的坐标为A(0,0,0)、
B(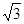 ,0,0)、C(
,0,0)、C(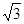 ,1,0)、D(0,1,0)、
,1,0)、D(0,1,0)、
|
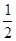 ,1),
,1),
从而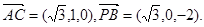
设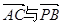 的夹角为θ,则
的夹角为θ,则
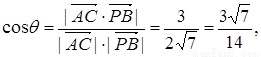
∴AC与PB所成角的余弦值为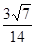 .
.
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,O,z),则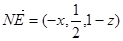 ,由NE⊥面PAC可得,
,由NE⊥面PAC可得,
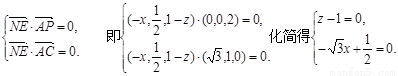 ∴
∴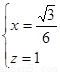
即N点的坐标为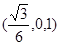 ,从而N点到AB、AP的距离分别为1,
,从而N点到AB、AP的距离分别为1,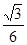 .
.
【解析】略

练习册系列答案
相关题目
 。
。 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且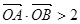 (其中O为原点),求k的取值范围。
(其中O为原点),求k的取值范围。