题目内容
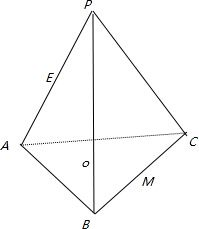 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP(1)求证:OE∥平面PBC
(2)若OE⊥PA,AB=3,求三棱锥P-ABC的体积.
分析:(1)证明:连接Ao延长交BC于M,连接PM,O是三角形的重心,可知AO=2OM,又AE=2EP,由三角形中位线可知OE∥PM,最后由线面平行的判定定理证明.
(2)如图:易证BC⊥平面PAM,所以三棱锥的体积转化为:三棱锥B-PAM和三棱锥C-PAM体积之和.
(2)如图:易证BC⊥平面PAM,所以三棱锥的体积转化为:三棱锥B-PAM和三棱锥C-PAM体积之和.
解答: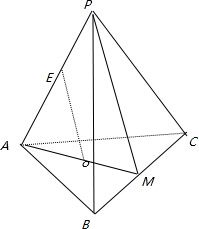 解:(1)证明:连接Ao延长交BC于M,连接PM,O是三角形的重心,
解:(1)证明:连接Ao延长交BC于M,连接PM,O是三角形的重心,
∴AO=2OM,又AE=2EP
∴OE∥PM
∴OE∥平面PBC
(2)由(1)知OE∥PM,OE⊥PA
∴PM⊥PA
在正三棱锥P-ABC中,M为中点
∴AM⊥BC
∴VP-ABC=
sPAM•BC=
 解:(1)证明:连接Ao延长交BC于M,连接PM,O是三角形的重心,
解:(1)证明:连接Ao延长交BC于M,连接PM,O是三角形的重心,∴AO=2OM,又AE=2EP
∴OE∥PM
∴OE∥平面PBC
(2)由(1)知OE∥PM,OE⊥PA
∴PM⊥PA
在正三棱锥P-ABC中,M为中点
∴AM⊥BC
∴VP-ABC=
| 1 |
| 3 |
9
| ||
| 8 |
点评:本题主要考查了立体几何中线面之间的位置关系及判定定理,还考查了在体积求解中的转化思想和害补法思想,属中档题

练习册系列答案
相关题目
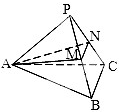 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
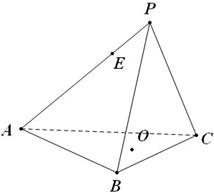 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是. 如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )
如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )