题目内容
 如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )
如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )分析:如图所示,过点P作PO⊥平面ABC,垂足为点O,则点O为正三角形ABC的中心,以点O为坐标原点,AO、OP所在直线分别为y轴、z轴的正方向建立空间直角坐标系.
不妨设AB=6,OP=3a.则A(0,-2
,0),B(3,
,0),C(-3,
,0),P(0,0,3a).设平面AMN的法向量为
=(x,y,z),则
,即可解得
.同理可得平面PBC的法向量
.利用平面AMN⊥平面PBC,可得
•
=0,解得a.取平面ABC的法向量为
=(0,0,1).利用cos<
,
>=
即可得出.
不妨设AB=6,OP=3a.则A(0,-2
| 3 |
| 3 |
| 3 |
| m |
|
| m |
| n |
| m |
| n |
| u |
| n |
| u |
| ||||
|
|
解答:解:如图所示,过点P作PO⊥平面ABC,垂足为点O,则点O为正三角形ABC的中心,以点O为坐标原点,AO、OP所在直线分别为y轴、z轴的正方向建立空间直角坐标系.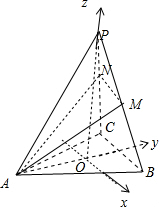
不妨设AB=6,OP=3a.则A(0,-2
,0),B(3,
,0),C(-3,
,0),P(0,0,3a).
=(3,
,-3a),
=(-3,
,-3a).
=(6,0,0).
∵
=
=(2,
,-2x),
=
=(-1,
,-a).
∴
=(2,
,a),
=(-1,
,2a).
∴
=(2,
,a),
=(-1,
,2a).
设平面AMN的法向量为
=(x,y,z),则
,
取y=
,解得x=-
,z=-
,可得
=(-
,
,-
).
同理可得平面PBC的法向量
=(0,
,
).
∵平面AMN⊥平面PBC,∴
•
=3-
=0,解得a2=
.
取平面ABC的法向量为
=(0,0,1).
则cos<
,
>=
=
=
=
=
.
故选D.

不妨设AB=6,OP=3a.则A(0,-2
| 3 |
| 3 |
| 3 |
| PB |
| 3 |
| PC |
| 3 |
| CB |
∵
| PM |
| 2 |
| 3 |
| PB |
2
| ||
| 3 |
| PN |
| 1 |
| 3 |
| PC |
| ||
| 3 |
∴
| OM |
2
| ||
| 3 |
| ON |
| ||
| 3 |
∴
| AM |
8
| ||
| 3 |
| AN |
7
| ||
| 3 |
设平面AMN的法向量为
| m |
|
取y=
| 3 |
| 9 |
| 5 |
| 22 |
| 5a |
| m |
| 9 |
| 5 |
| 3 |
| 22 |
| 5a |
同理可得平面PBC的法向量
| n |
| 3 |
| 1 |
| a |
∵平面AMN⊥平面PBC,∴
| m |
| n |
| 22 |
| 5a2 |
| 22 |
| 15 |
取平面ABC的法向量为
| u |
则cos<
| n |
| u |
| ||||
|
|
| ||||
|
| 1 | ||
|
| 1 | ||||
|
| ||
| 9 |
故选D.
点评:本题考查了通过建立空间直角坐标系、利用平面的法向量的夹角解决空间角问题,属于难题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
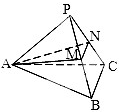 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
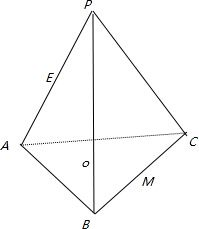 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP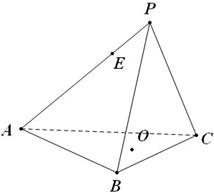 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.