题目内容
设函数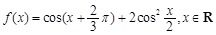 .
.
(1)求 的值域;
的值域;
(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若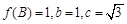 ,求a的值.
,求a的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据两角和的余弦公式展开,再根据二倍角公式中的降幂公式 展开,然后合并同类项,利用
展开,然后合并同类项,利用 进行化简;利用三角函数的有界性求出值域.
进行化简;利用三角函数的有界性求出值域.
(2)若 ,
,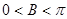 ,得到角
,得到角 的取值,方法一:可以利用余弦定理
的取值,方法一:可以利用余弦定理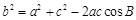 ,将已知代入,得到关于
,将已知代入,得到关于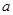 的方程,方法二:利用正弦定理
的方程,方法二:利用正弦定理 ,先求
,先求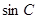 ,再求角C,然后利用特殊三角形,得到
,再求角C,然后利用特殊三角形,得到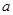 的值.
的值.
试题解析:(1)
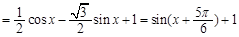 4分
4分
因此 的值域为[0,2]. 6分
的值域为[0,2]. 6分
(2)由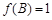 得
得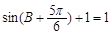 ,
,
即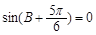 ,又因
,又因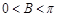 ,故
,故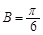 . 9分
. 9分
解法1:由余弦定理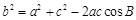 ,得
,得 ,
,
解得 . 12分
. 12分
解法2:由正弦定理 ,得
,得 . 9分
. 9分
当 时,
时, ,从而
,从而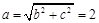 ; 10分
; 10分
当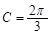 时,
时,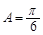 ,又
,又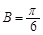 ,从而
,从而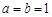 . 11分
. 11分
故a的值为1或2. 12分
考点:两角和的余弦公式、二倍角公式、余弦定理、正弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
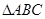 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若 .
. ,求函数
,求函数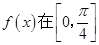 上的取值范围.
上的取值范围. 中,
中, 分别是角
分别是角 所对的边,且满足
所对的边,且满足 .
. 的大小;
的大小; ,求
,求 的最小值.
的最小值. 中,角
中,角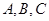 的对边分别为
的对边分别为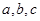 ,设S为△ABC的面积,满足4S=
,设S为△ABC的面积,满足4S=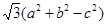 .
. 的大小;(2)若
的大小;(2)若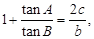 且
且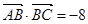 求
求 的值.
的值. 上的两点,点C是圆
上的两点,点C是圆 轴的正半轴的交点,将锐角
轴的正半轴的交点,将锐角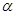 的终边
的终边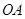 按逆时针方向旋转
按逆时针方向旋转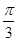 到
到 .
.
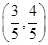 ,求
,求 的值;
的值; ,并求
,并求 ,且
,且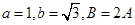 。
。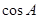 的值;(2)求c的值。
的值;(2)求c的值。 所对的边分别为
所对的边分别为 ,且
,且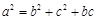 .
.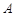 的大小;
的大小;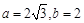 ,求边
,求边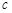 的值.
的值.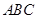 中,角
中,角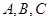 所对的边分别为
所对的边分别为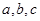 ,已知
,已知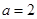 ,
,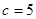 ,
,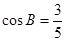 .
.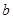 的值;
的值; 的值.
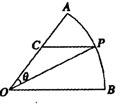
的值.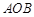 ,圆心角
,圆心角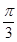 ,半径为2,在半径
,半径为2,在半径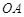 上有一动点
上有一动点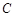 ,过点
,过点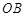 的直线交弧
的直线交弧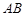 于点
于点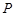 .
.
 的长;
的长; ,求
,求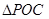 面积的最大值及此时
面积的最大值及此时 的值.
的值.