题目内容
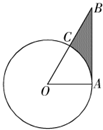 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )分析:先求出△OAB的面积,然后求出扇形OAC的面积,阴影部分的面积=S△OAB-S扇形OAC即可得出答案.
解答:解:∵AB是⊙O的切线,切点为A,
∴OA⊥AB,
∴AB=OAtan∠AOB=
∴S△OAB=
OA•AB=
×1×
=
S扇形OAC=
=
∴阴影部分的面积=S△OAB-S扇形OAC=
-
故选:A.
∴OA⊥AB,
∴AB=OAtan∠AOB=
| 3 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
S扇形OAC=
| 60π×12 |
| 360 |
| π |
| 6 |
∴阴影部分的面积=S△OAB-S扇形OAC=
| ||
| 2 |
| π |
| 6 |
故选:A.
点评:此题考查了扇形面积公式及切线的性质,解答本题的关键是求出AB的长度,属于基础题.

练习册系列答案
相关题目
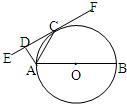 如图,AB是⊙O的直径,EF切⊙O于C,AD⊥EF于D,AD=2,AB=8,则AC的长为( )
如图,AB是⊙O的直径,EF切⊙O于C,AD⊥EF于D,AD=2,AB=8,则AC的长为( )| A、2 | ||
| B、4 | ||
C、2
| ||
| D、3 |
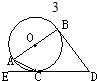 12、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是
12、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是
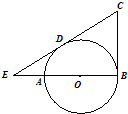 如图,AB是⊙O的直径,CB切⊙O于点B,CD切⊙O于点D,CD交BA的延长线于点E.若AB=3,ED=2,则BC的长为
如图,AB是⊙O的直径,CB切⊙O于点B,CD切⊙O于点D,CD交BA的延长线于点E.若AB=3,ED=2,则BC的长为 【选修4-1:几何证明选讲】
【选修4-1:几何证明选讲】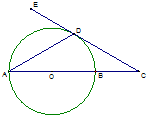 (2012•东城区一模)如图,AB是⊙O的直径,直线DE切⊙O于点D,且与AB延长线交于点C,若CD=
(2012•东城区一模)如图,AB是⊙O的直径,直线DE切⊙O于点D,且与AB延长线交于点C,若CD=