题目内容
如果两个椭圆的离心率相等,那么就称这两个椭圆相似.已知椭圆C与椭圆![]() 相似,且椭圆C的一个短轴端点是抛物线
相似,且椭圆C的一个短轴端点是抛物线![]() 的焦点.
的焦点.
(Ⅰ)试求椭圆C的标准方程;
(Ⅱ)设椭圆E的中心在原点,对称轴在坐标轴上,直线l∶y=kx+t(k≠0,t≠0)与椭圆C交于A,B两点,且与椭圆E交于H,K两点.若线段AB与线段HK的中点重合,试判断椭圆C与椭圆E是否为相似椭圆?并证明你的判断.
答案:
解析:
解析:
解析:(Ⅰ)椭圆![]() 的离心率为
的离心率为![]() 1分
1分
抛物线![]() 的焦点为
的焦点为![]() . 2分
. 2分
设椭圆![]() 的方程为
的方程为![]() ,
,
由题意,得: 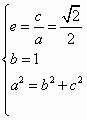 ,解得
,解得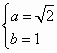 ,
,
∴椭圆![]() 的标准方程为
的标准方程为 ![]() . 5分
. 5分
(Ⅱ)解法一:椭圆![]() 与椭圆
与椭圆![]() 是相似椭圆. 6分
是相似椭圆. 6分
联立椭圆![]() 和直线
和直线![]() 的方程,
的方程,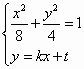 ,消去
,消去![]() ,
,
得![]() , 7分
, 7分
设![]() 的横坐标分别为
的横坐标分别为![]() ,则
,则![]() . 8分
. 8分
设椭圆![]() 的方程为
的方程为![]() , 9分
, 9分
联立方程组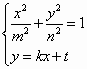 ,消去
,消去![]() ,得
,得![]() ,
,
设![]() 的横坐标分别为
的横坐标分别为![]() ,则
,则![]() . 10分
. 10分
∵弦![]() 的中点与弦
的中点与弦![]() 的中点重合, 11分
的中点重合, 11分
∴![]()
![]() ,
,![]()
![]() ,
,
∵![]() ,∴化简得
,∴化简得![]() , 11分
, 11分
求得椭圆![]() 的离心率
的离心率![]() , 12分
, 12分
∴椭圆![]() 与椭圆
与椭圆![]() 是相似椭圆.
是相似椭圆.
解法二:设椭圆![]() 的方程为
的方程为![]() ,
,
并设![]() .
.
∵![]() 在椭圆
在椭圆![]() 上,
上,
∴![]() 且
且![]() ,两式相减变恒等变形得
,两式相减变恒等变形得![]() . 7分
. 7分
由![]() 在椭圆
在椭圆![]() 上,仿前述方法可得
上,仿前述方法可得![]() . 10分
. 10分
∵弦![]() 的中点与弦
的中点与弦![]() 的中点重合,
的中点重合,
∴![]() , 12分
, 12分
求得椭圆![]() 的离心率
的离心率![]() , 10分
, 10分
∴椭圆![]() 与椭圆
与椭圆![]() 是相似椭圆.
是相似椭圆.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 与椭圆
与椭圆 相似,且椭圆
相似,且椭圆 的焦点.
的焦点. 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线 与椭圆
与椭圆 两点,且与椭圆
两点,且与椭圆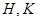 两点.若线段
两点.若线段 与线段
与线段 的中点重合,试判断椭圆
的中点重合,试判断椭圆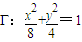 相似,且椭圆C的一个短轴端点是抛物线
相似,且椭圆C的一个短轴端点是抛物线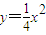 的焦点.
的焦点.