题目内容
没有公共点的两条直线a、b与平面 α 所成角都相等,则直线a、b的位置关系是
平行或异面
平行或异面
.分析:因为直线a、b没有公共点,所以不可能为相交直线,分a,b平行和异面两种情况讨论是否会出现a,b与平面α所成角相等的情况,当a,b平行时,容易判断,当a,b为异面直线时,可先a上的一点A作b的平行线b′,通过判断a与b′所成角是否有相等的情况,来判断a与b的情况.
解答:解:∵直线a,b平行时,它们与平面 α 所成角必定相等,∴直线a、b可以为平行直线.
当直线a,b是异面直线时,如图,,过a上的一点A作b的平行线b′,
则当∠E=∠F时,直线a与b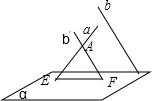 ′与平面α所称角相等.
′与平面α所称角相等.
∵b∥b′,∴直线b,b′与平面α所成角相等,
∴直线a,b是异面直线时,也可以与平面α所成角相等,
∴直线a、b的位置关系是平行或异面.
故答案为:平行或异面
当直线a,b是异面直线时,如图,,过a上的一点A作b的平行线b′,
则当∠E=∠F时,直线a与b
 ′与平面α所称角相等.
′与平面α所称角相等.∵b∥b′,∴直线b,b′与平面α所成角相等,
∴直线a,b是异面直线时,也可以与平面α所成角相等,
∴直线a、b的位置关系是平行或异面.
故答案为:平行或异面
点评:本题主要考查了空间两条直线位置关系的判断,以及直线与平面位置关系的判断,综合考查了学生的空间想象力,推理能力.

练习册系列答案
相关题目