题目内容
在三棱锥O-ABC中,三条棱OA、OB、OC两两互相垂直,且OA=OB=OC,M是AB的中点,则OM与平面ABC所成角的大小是分析:由题意画出图象,由于三条棱OA、OB、OC两两互相垂直,且OA=OB=OC,所以定点O在底面的投影为底面△ABC的中心即为D,连接OD,
OM,在直角△OMD中求解即可.
OM,在直角△OMD中求解即可.
解答: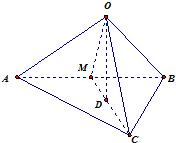 解:在三棱锥O-ABC中,三条棱OA,OB,OC两两互相垂直,
解:在三棱锥O-ABC中,三条棱OA,OB,OC两两互相垂直,
且OA=OB=OC,M是AB边的中点,
设|OA|=a,则|AB|=|BC|=|CA|=
a,VO-ABC=
a3,
O点在底面的射影为底面△ABC的中心,
|OD|=
=
a,又|DM|=
|MC|=
a,
OM与平面ABC所成角的正切是tanθ=
=
,
故答案为:arctan
.
 解:在三棱锥O-ABC中,三条棱OA,OB,OC两两互相垂直,
解:在三棱锥O-ABC中,三条棱OA,OB,OC两两互相垂直,且OA=OB=OC,M是AB边的中点,
设|OA|=a,则|AB|=|BC|=|CA|=
| 2 |
| 1 |
| 6 |
O点在底面的射影为底面△ABC的中心,
|OD|=
| VO-ABC | ||
|
| ||
| 3 |
| 1 |
| 3 |
| ||
| 6 |
OM与平面ABC所成角的正切是tanθ=
| ||||
|
| 2 |
故答案为:arctan
| 2 |
点评:此题重点考查了三条侧棱两两垂直则顶点在底面的投影为底部三角形的垂心,三条侧棱长相等,则顶点在底面的投影为底部三角形的外心,故为其中心这一结论,另外还考查了直线与平面所成角的概念及反三角知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
