题目内容
设函数f(x)的导函数为f′(x),若f(x)=ax3-ax2+[(1)用a表示f′(1);
(2)若函数f(x)在R上存在极大值和极小值,求a的取值范围;
(3)在(2)条件下函数f(x)在x∈[1,+∞]单调递增,求a的取值范围.
解析:(1)∵f′(x)=3ax2-2ax+[![]() -1]
-1]
∴f′(1)=a+![]() -1.
-1.
即f′(1)=2a-2.
(2)∵f(x)=ax3-ax2+(a-2)x,
f′(x)=3ax2-2ax+(a-2).
若f(x)存在极大值和极小值,则在R上f′(x)=0有两个不等的实根,
即Δ=4a2-12a(a-2)=24a-8a2>0,得0<a<3.
(3)由f′(x)=0,得x=![]() =
=![]() .依题意由
.依题意由![]() ≤1,得a≥1.
≤1,得a≥1.
又0<a<3,∴1≤a<3.

练习册系列答案
相关题目
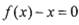 有实数根;
有实数根;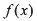 的导数
的导数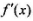 (满足
(满足 ”
” 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;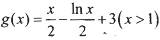 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;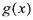 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在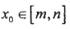 ,使得
,使得 ”,请利用函数
”,请利用函数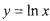 的图象说明这一结论.
的图象说明这一结论.