题目内容
设M是由满足下列条件的函数f(X)构成的集合:
①方程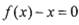 有实数根;
有实数根;
②函数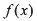 的导数
的导数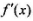 (满足
(满足 ”
”
(I )若函数 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;
(II) 判断函^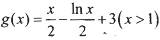 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(III) “对于(II)中函数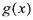 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在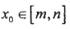 ,使得
,使得 ”,请利用函数
”,请利用函数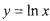 的图象说明这一结论.
的图象说明这一结论.
【答案】
(Ⅰ)令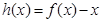 ,则
,则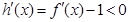 ,即
,即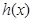 在区间
在区间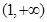 上单调递减
上单调递减
所以,使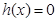 ,即
,即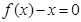 成立的
成立的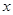 至多有一解,┄┄┄┄┄┄┄┄┄3分
至多有一解,┄┄┄┄┄┄┄┄┄3分
又由题设①知方程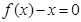 有实数根,
有实数根,
所以,方程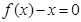 只有一个实数根;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分
只有一个实数根;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分
(Ⅱ)由题意易知,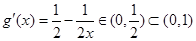 ,满足条件②┄┄┄┄┄┄┄┄┄6分
,满足条件②┄┄┄┄┄┄┄┄┄6分
令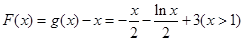 ,
,
则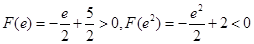 ,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分
,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分
又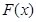 在区间
在区间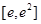 上连续,所以
上连续,所以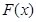 在
在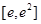 上存在零点
上存在零点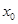 ,
,
即方程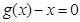 有实数根
有实数根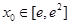 ,故
,故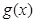 满足条件①,
满足条件①,
综上可知,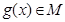 ;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分
;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分
(Ⅲ)由(Ⅱ)知: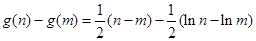 ,
,
而 ,
,
所以原式等价于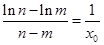 ,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄11分
,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄11分
该等式说明函数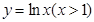 上任意两点
上任意两点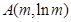 和
和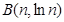 的连线段
的连线段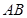 (如图所示),在曲线
(如图所示),在曲线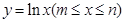 上都一定存在一点
上都一定存在一点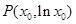 ,使得该点 处的切线平行于
,使得该点 处的切线平行于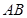 ,根据
,根据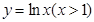 图象知该等式一定成立.
图象知该等式一定成立.
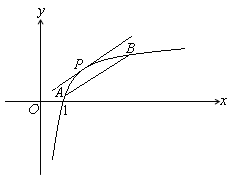
【解析】略

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目