题目内容
 (2012•杭州二模)已知扇形的圆心角为2θ(0<θ<
(2012•杭州二模)已知扇形的圆心角为2θ(0<θ<| π |
| 4 |
| 1 |
| 2 |
r2tan
| θ |
| 2 |
r2tan
.| θ |
| 2 |
分析:将图二可拆分成两个图一的形式,可以类比得到结论.图一角是2α,图二拆分后角是α,故矩形面积的最大值为
r2tan
,由此可得结论.
| 1 |
| 2 |
| θ |
| 2 |
解答: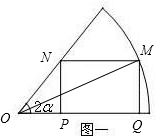 解:图一,设∠MOQ=x,则MQ=rsinx
解:图一,设∠MOQ=x,则MQ=rsinx
在△OMN中,
=
,∴MN=
∴矩形面积S=
=
[cos(2x-2α)-cos2α]≤
[1-cos2α]=
r2tanα
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为
r2tanθ,图二可拆分成两个,
图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为
r2tan
,
而图二时由两个这样的图形组成,所以两个则为r2tan
.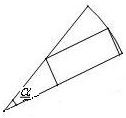
故答案为:r2tan
 解:图一,设∠MOQ=x,则MQ=rsinx
解:图一,设∠MOQ=x,则MQ=rsinx在△OMN中,
| MN |
| sin(2α-x) |
| r |
| sin(180°-2α) |
| rsin(2α-x) |
| sin2α |
∴矩形面积S=
| r2sin(2α-x) sinx |
| sin2α |
| r2 |
| 2sin2α |
| r2 |
| 2sin2α |
| 1 |
| 2 |
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为
| 1 |
| 2 |
图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为
| 1 |
| 2 |
| θ |
| 2 |
而图二时由两个这样的图形组成,所以两个则为r2tan
| θ |
| 2 |

故答案为:r2tan
| θ |
| 2 |
点评:本题考查扇形内接矩形面积问题,考查学生分析解决问题的能力,解题的关键是发现两个图之间的联系,利用已有的结论进行解题.

练习册系列答案
相关题目
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为