题目内容
给定方程: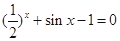 ,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若
,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若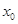 是该方程的实数解,则
是该方程的实数解,则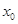
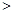 –1.则正确命题是 .
–1.则正确命题是 .
②③④
解析试题分析:由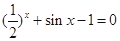 得
得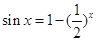 ,令
,令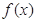 =
=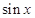 ,
,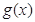 =
=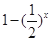 ,在同一坐标系中画出两函数的图像如右,由图像知:①错,③、④对,而由于
,在同一坐标系中画出两函数的图像如右,由图像知:①错,③、④对,而由于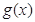 =
=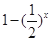 递增,小于1,且以直线
递增,小于1,且以直线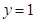 为渐近线,
为渐近线,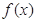 =
=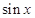 在-1到1之间振荡,故在区间(0,+¥)上,两者图像有无穷多个交点,所以②对,故选填②③④.
在-1到1之间振荡,故在区间(0,+¥)上,两者图像有无穷多个交点,所以②对,故选填②③④.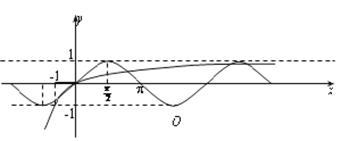
考点:函数的零点;方程的根;正弦函数的图像;指数函数的图像。
点评:把方程根的个数转化为函数图像的交点的个数是做本题的关键。本题就是把方程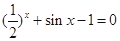 的根转化为函数
的根转化为函数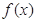 =
=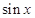 和函数
和函数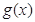 =
=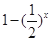 的交点进行解决的,考查了学生分析问题、解决问题的能力,同时也考查了学生的数形结合思想,对学生的能力要求较高。
的交点进行解决的,考查了学生分析问题、解决问题的能力,同时也考查了学生的数形结合思想,对学生的能力要求较高。

练习册系列答案
相关题目
 满足
满足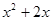 (x≥0),若
(x≥0),若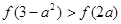 ,则实数
,则实数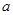 的取值范围是________.
的取值范围是________.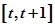 上满足不等式
上满足不等式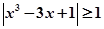 的解有且只有一个,则实数
的解有且只有一个,则实数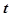 的取值范围是_________。
的取值范围是_________。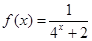 ,利用课本中推导等差数列前
,利用课本中推导等差数列前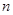 项和公式的方法,可求得
项和公式的方法,可求得 的值是________________;
的值是________________; 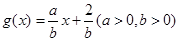 和函数
和函数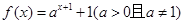 的图象恒过同一个定点,则
的图象恒过同一个定点,则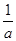 +
+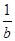 的最小值为________.
的最小值为________. 的值为 .
的值为 .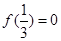 ,则不等式
,则不等式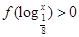 的解集是
的解集是  有负数根,则实数
有负数根,则实数 的取值范围是 .
的取值范围是 . ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
, ,若直线
,若直线 与函数
与函数 的图象有三个不同的交点,则
的图象有三个不同的交点,则 的取值范围是__________.
的取值范围是__________.