题目内容
设事件A表示“关于x的方程x2+2ax+b2=0有实数根”.
(1)若a、b∈{1,2,3},求事件A发生的概率P(A);
(2)若a、b∈[1,3],求事件A发生的概率P(A).
(1)若a、b∈{1,2,3},求事件A发生的概率P(A);
(2)若a、b∈[1,3],求事件A发生的概率P(A).
分析:(1)先求出关于x的方程x2+2ax+b2=0有实数根的条件,求出数对(a,b)的所有可能事件,再求出求出事件A包含的事件,根据公式计算即可;
(2)先判断为几何概型,利用面积比计算即可.
(2)先判断为几何概型,利用面积比计算即可.
解答:解:(1)由关于x的方程x2+2ax+b2=0有实数根,得△≥0.
∴4a2-4b2≥0,故a2≥b2,当a>0,b>0时,得a≥b.
若a、b∈{1,2,3},则总的基本事件数(即有序实数对(a,b)的个数)
为3×3=9.事件A包含的基本事件为:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),共有6个.
∴事件A发生的概率P(A)=
=
.
(2)若a、b∈[1,3],则总的基本事件所构成的区域Ω={(a,b)|1≤a≤3,1≤b≤3},是平面直角坐标系aOb中的一个正方形
如图: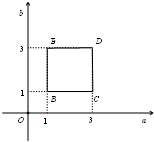
其面积SΩ=( 3-1 )2=4.
事件A构成的区域是A={(a,b)|1≤a≤3,1≤b≤3,a≥b},
是平面直角坐标系aOb中的一个等腰直角三角形,如图
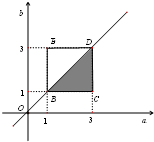 的阴影部分,
的阴影部分,
其面积SA=
×( 3-1 )2=2.
故事件A发生的概率P(A)=
=
=
.
∴4a2-4b2≥0,故a2≥b2,当a>0,b>0时,得a≥b.
若a、b∈{1,2,3},则总的基本事件数(即有序实数对(a,b)的个数)
为3×3=9.事件A包含的基本事件为:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),共有6个.
∴事件A发生的概率P(A)=
| 6 |
| 9 |
| 2 |
| 3 |
(2)若a、b∈[1,3],则总的基本事件所构成的区域Ω={(a,b)|1≤a≤3,1≤b≤3},是平面直角坐标系aOb中的一个正方形
如图:

其面积SΩ=( 3-1 )2=4.
事件A构成的区域是A={(a,b)|1≤a≤3,1≤b≤3,a≥b},
是平面直角坐标系aOb中的一个等腰直角三角形,如图
 的阴影部分,
的阴影部分,其面积SA=
| 1 |
| 2 |
故事件A发生的概率P(A)=
| SA |
| SΩ |
| 2 |
| 4 |
| 1 |
| 2 |
点评:本题考查古典概型的概率计算及几何概型的概率计算.

练习册系列答案
相关题目
 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设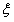 表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;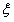 的数学期望E
的数学期望E ;
;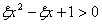 的解集是实数集R”为事件A,求事件A发生的概率P(A)。
的解集是实数集R”为事件A,求事件A发生的概率P(A)。