题目内容
已知A、B是△ABC内角，
（1）若A、B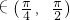
，求证：tanA•tanB＞1；
（2）若B=
，求sinA+sinC的取值范围．
（本小题满分12分）
解：（1）证明：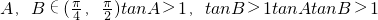
．--------（4分）
（2）
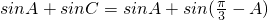，--------（5分）
=
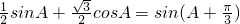--------（7分）
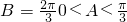--------（8分）
．--------（10分）
∴sinA+sinC的取值范围是
--------（12分）
分析：（1）直接通过角的范围，判断tanA和tanB的范围，推出结果．
（2）通过角的转化化简表达式为A的三角函数，结合A的范围求出表达式的范围即可．
点评：本题考查三角函数的值的判断，三角函数值域的范围的求法，考查计算能力．
解：（1）证明：
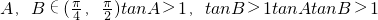．--------（4分）（2）
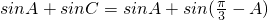，--------（5分）=
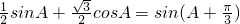--------（7分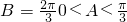）--------（8分）．--------（10分）∴sinA+sinC的取值范围是
--------（12分）分析：（1）直接通过角的范围，判断tanA和tanB的范围，推出结果．
（2）通过角的转化化简表达式为A的三角函数，结合A的范围求出表达式的范围即可．
点评：本题考查三角函数的值的判断，三角函数值域的范围的求法，考查计算能力．
练习册系列答案
相关题目