题目内容
据某城市2002年末所作的统计资料显示,到2002年末,该城市堆积的垃圾已达50万吨,侵占了大量的土地,并且成为造成环境污染的因素之一.根据预测,从2003年起该城市还将以每年3万吨的速度产生新的垃圾,垃圾的资源化和回收处理已经成为该市城市建设中的重要问题.(1)假设1992年底该城市堆积的垃圾为10万吨,从1993年到2002年这十年中,该城市每年产生的新垃圾以8%的年平均增长率增长,试求1993年该城市产生的新垃圾约有多少万吨?(精确到0.01,参考数据:1.0810≈2.159)
(2)如果从2003年起,该市每年处理上年堆积垃圾的20%,现有b1表示2003年底该市堆积的垃圾数量,b2表示2004年底该市堆积的垃圾数量…bn表示2002+n年底该城市堆积的垃圾数量,①求b1;②试归纳出bn的表达式(不用证明);③计算
| lim | n→∞ |
分析:(1)要求1993年该城市产生的新垃圾约有多少万吨,我们可以设1993年该城市产生的新垃圾约有X万吨,然后由1992年底该城市堆积的垃圾为10万吨,从1993年到2002年这十年中,该城市每年产生的新垃圾以8%的年平均增长率增长,到2002年末,该城市堆积的垃圾已达50万吨,构造关于X的方程,解方程,即可得到结果.
(2)由2002年末,该城市堆积的垃圾已达50万吨,从2003年起,该市每年处理上年堆积垃圾的20%,现有b1表示2003年底该市堆积的垃圾数量,我们易代入得到bn=50×(
)n+3×(
)n-1+3×(
)n-2++3×
+3,然后利用极限思想,求出
bn的值.
(2)由2002年末,该城市堆积的垃圾已达50万吨,从2003年起,该市每年处理上年堆积垃圾的20%,现有b1表示2003年底该市堆积的垃圾数量,我们易代入得到bn=50×(
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| lim |
| n→∞ |
解答:解:(1)设1993年该城市产生的新垃圾为x万吨.依题意,得
10+x+1.08x+1.082x++1.089x=50,
∴
•x=40.
∴x=
×40≈2.76万吨.
∴1993年该城市产生的新垃圾约为2.76万吨.
(2)①b1=50×80%+3=43(万吨).
②∵b1=50×80%+3=50×
+3,
b2=
b1+3=50×(
)2+3×
+3,
b3=
b2+3=50×(
)3+3×(
)2+3×
+3,
∴可归纳出bn=50×(
)n+3×(
)n-1+3×(
)n-2++3×
+3
=50×(
)n+3×
=50×(
)n+15[1-(
)n]=35×(
)n+15.
③
bn=
[35×(
)n+15]=15.
这说明,按题目设想的方法处理垃圾,该市垃圾总量将逐年减少,但不会少于15万吨.
10+x+1.08x+1.082x++1.089x=50,
∴
| 1-1.0810 |
| 1-1.08 |
∴x=
| 0.08 |
| 1.0810-1 |
∴1993年该城市产生的新垃圾约为2.76万吨.
(2)①b1=50×80%+3=43(万吨).
②∵b1=50×80%+3=50×
| 4 |
| 5 |
b2=
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
b3=
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
∴可归纳出bn=50×(
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
=50×(
| 4 |
| 5 |
1-(
| ||
1-
|
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
③
| lim |
| n→∞ |
| lim |
| n→∞ |
| 4 |
| 5 |
这说明,按题目设想的方法处理垃圾,该市垃圾总量将逐年减少,但不会少于15万吨.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
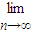 bn,并说明其实际意义.
bn,并说明其实际意义.