题目内容
(本题满分12分)
已知函数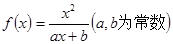 ,且方程
,且方程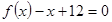 有两个实根
有两个实根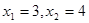 .
.
(1)求函数 的解析式;
的解析式;
(2)设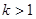 ,解关于
,解关于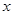 的不等式
的不等式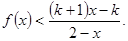
【答案】
(1) ;(2)当
;(2)当 时,解集为
时,解集为 ;当
;当 时,不等式为
时,不等式为 ,解集为
,解集为 ;当
;当 时,解集为
时,解集为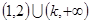 .
.
【解析】
试题分析:(1)将 分别代入方程
分别代入方程 ,得
,得
解得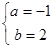 ,
-------2分 所以
,
-------2分 所以 --------4分
--------4分
(2)不等式即为 ,可化为
,可化为
即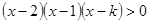 --------6分
--------6分
当 时,解集为
时,解集为 ;
-------- 8分
;
-------- 8分
当 时,不等式为
时,不等式为 ,解集为
,解集为 ; ----- 10分
; ----- 10分
当 时,解集为
时,解集为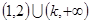 .
----------12分
.
----------12分
考点:分式不等式的解法;一元二次不等式的解法;二次函数的性质。
点评:解含参二次不等式的主要思想是分类讨论:一般的讨论开口方向、两根的大小和判别式。在分类讨论时要注意不重不漏。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面