题目内容
已知圆C:(x-3)2+(y-4)2=4和直线l:kx-y-4k+3=0(1)求证:不论k取什么值,直线和圆总相交;
(2)求k取何值时,圆被直线截得的弦最短,并求最短弦的长.
【答案】分析:(1)由直线l的方程y-3=k(x-4)可得直线l恒通过定点(4,3),而点(4,3)在圆的内部,故直线l与圆C总相交.
(2)先求出圆心到直线l的距离为d,设弦长为L,则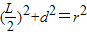 ,再根据L的解析式,利用基本不等式求得
,再根据L的解析式,利用基本不等式求得
L的最小值.
解答:解:(1)证明:由直线l的方程可得y-3=k(x-4),则直线l恒通过定点(4,3),把(4,3)代入圆C的方程,得(4-3)2+(3-4)2=2<4,
所以点(4,3)在圆的内部,所以直线l与圆C总相交.
(2)设圆心到直线l的距离为d,则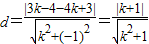 ,
,
又设弦长为L,则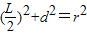 ,即
,即 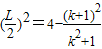 =4-(1+
=4-(1+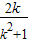 )=3-
)=3-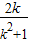 ≥2.
≥2.
∴当k=1时,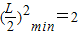 ,
,
∴Lmin=2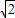 ,所以圆被直线截得最短的弦长为2
,所以圆被直线截得最短的弦长为2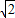 .
.
点评:本题主要考查直线过定点问题,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.
(2)先求出圆心到直线l的距离为d,设弦长为L,则
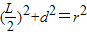 ,再根据L的解析式,利用基本不等式求得
,再根据L的解析式,利用基本不等式求得L的最小值.
解答:解:(1)证明:由直线l的方程可得y-3=k(x-4),则直线l恒通过定点(4,3),把(4,3)代入圆C的方程,得(4-3)2+(3-4)2=2<4,
所以点(4,3)在圆的内部,所以直线l与圆C总相交.
(2)设圆心到直线l的距离为d,则
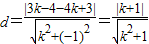 ,
,又设弦长为L,则
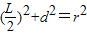 ,即
,即 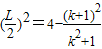 =4-(1+
=4-(1+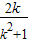 )=3-
)=3-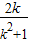 ≥2.
≥2.∴当k=1时,
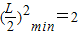 ,
,∴Lmin=2
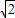 ,所以圆被直线截得最短的弦长为2
,所以圆被直线截得最短的弦长为2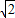 .
.点评:本题主要考查直线过定点问题,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
相关题目
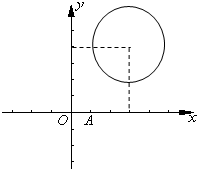 已知圆C:(x-3)2+(y-4)2=4,
已知圆C:(x-3)2+(y-4)2=4,