题目内容
已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).(Ⅰ)若l1与圆相切,求l1的方程;
(Ⅱ)若l1与圆相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,求证:AM•AN为定值.
分析:(I)由直线l1与圆相切,则圆心到直线的距离等于半径,求得直线方程,注意分类讨论;
(II)分别联立相应方程,求得M,N的坐标,再求AM•AN.
(II)分别联立相应方程,求得M,N的坐标,再求AM•AN.
解答:解:(Ⅰ)①若直线l1的斜率不存在,即直线x=1,符合题意.(2分)
②若直线l1斜率存在,设直线l1为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即
=2解之得k=
.
所求直线方程是x=1,3x-4y-3=0.(5分)
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0
由
得N(
,-
)又直线CM与l1垂直,
得M(
,
).
∴AM*AN=
•
=6为定值.(10分)
②若直线l1斜率存在,设直线l1为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即
| |3k-4-k| | ||
|
| 3 |
| 4 |
所求直线方程是x=1,3x-4y-3=0.(5分)
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0
由
|
| 2k-2 |
| 2k+1 |
| 3k |
| 2k+1 |
|
| k2+4k+3 |
| 1+k2 |
| 4k2+2k |
| 1+k2 |
∴AM*AN=
| 2 |2k+1| |
| 1+k2 |
| 1+k2 |
3
| ||
| |2k+1| |
点评:本题主要考查直线与圆的位置关系以及直线与直线的交点和两点间的距离公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
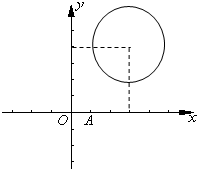 已知圆C:(x-3)2+(y-4)2=4,
已知圆C:(x-3)2+(y-4)2=4,