题目内容
某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
解:设进水量选第x级,则t小时后水塔中水的剩余量为:
y=100+10xt-10t-100 ,且0≤t≤16.
,且0≤t≤16.
根据题意0<y≤300,∴0<100+10xt-10t-100 ≤300.
≤300.
当t=0时,结论成立.
当t>0时,由左边得x>1+10( )
)
令m= ,由0<t≤16,m≥
,由0<t≤16,m≥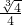 ,
,
记f(t)=1+10( )=1+10m2-10m3,(m≥
)=1+10m2-10m3,(m≥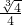 ),
),
则f′(t)=20m-30 m 2=0得m=0或m= .
.
∵当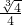 ≤m<
≤m< 时,f′(t)>0;当m>
时,f′(t)>0;当m> 时,f′(t)<0,
时,f′(t)<0,
∴所以m= 时(此时t=
时(此时t=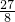 ),f(t)最大值=1+10(
),f(t)最大值=1+10( )2-10(
)2-10( )3=
)3=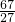 ≈2.48.
≈2.48.
当t=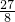 时,1+10(
时,1+10( )有最大值2.48.∴x>2.48,即x≥3.
)有最大值2.48.∴x>2.48,即x≥3.
由右边得x≤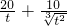 +1,
+1,
当t=16时,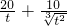 +1取最小值
+1取最小值 +1=
+1= ∈(3,4).
∈(3,4).
即x≤3.
综合上述,进水量应选为第3级.
分析:解决本题的关键是水塔中的水不空又不会使水溢出,其存水量的平衡与进水量、选择的进水级别与进水时间相关,而出水量有生活用水与工业用水两部分构成,故水塔中水的存量是一个关于进水级别与用水时间的函数.因此设进水量选第x级,t小时后水塔中水的剩余量为:y=100+10xt-10t-100 ,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10(
,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10( ).再令m=
).再令m= ,以m为单位得到函数y=1+10m2-10m3,(m≥
,以m为单位得到函数y=1+10m2-10m3,(m≥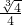 ),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤
),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤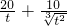 +1,类似于前面的讨论得出x≤3,从而最终得出x=3.
+1,类似于前面的讨论得出x≤3,从而最终得出x=3.
点评:本题以函数在实际生活中的应用为例,考查了导数在最大值、最小值问题中的应用,属于难题.着重考查数学建模的基本思想,怎么样把实际问题转化为数学问题,进而用已有的数学知识求这个问题的解.在解题过程中运用了化二元为一元,化为基本初等函数的数学思想.
y=100+10xt-10t-100
 ,且0≤t≤16.
,且0≤t≤16.根据题意0<y≤300,∴0<100+10xt-10t-100
 ≤300.
≤300.当t=0时,结论成立.
当t>0时,由左边得x>1+10(
 )
)令m=
 ,由0<t≤16,m≥
,由0<t≤16,m≥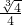 ,
,记f(t)=1+10(
 )=1+10m2-10m3,(m≥
)=1+10m2-10m3,(m≥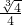 ),
),则f′(t)=20m-30 m 2=0得m=0或m=
 .
.∵当
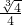 ≤m<
≤m< 时,f′(t)>0;当m>
时,f′(t)>0;当m> 时,f′(t)<0,
时,f′(t)<0,∴所以m=
 时(此时t=
时(此时t=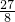 ),f(t)最大值=1+10(
),f(t)最大值=1+10( )2-10(
)2-10( )3=
)3=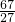 ≈2.48.
≈2.48.当t=
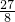 时,1+10(
时,1+10( )有最大值2.48.∴x>2.48,即x≥3.
)有最大值2.48.∴x>2.48,即x≥3.由右边得x≤
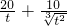 +1,
+1,当t=16时,
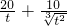 +1取最小值
+1取最小值 +1=
+1= ∈(3,4).
∈(3,4).即x≤3.
综合上述,进水量应选为第3级.
分析:解决本题的关键是水塔中的水不空又不会使水溢出,其存水量的平衡与进水量、选择的进水级别与进水时间相关,而出水量有生活用水与工业用水两部分构成,故水塔中水的存量是一个关于进水级别与用水时间的函数.因此设进水量选第x级,t小时后水塔中水的剩余量为:y=100+10xt-10t-100
 ,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10(
,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10( ).再令m=
).再令m= ,以m为单位得到函数y=1+10m2-10m3,(m≥
,以m为单位得到函数y=1+10m2-10m3,(m≥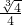 ),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤
),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤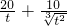 +1,类似于前面的讨论得出x≤3,从而最终得出x=3.
+1,类似于前面的讨论得出x≤3,从而最终得出x=3.点评:本题以函数在实际生活中的应用为例,考查了导数在最大值、最小值问题中的应用,属于难题.着重考查数学建模的基本思想,怎么样把实际问题转化为数学问题,进而用已有的数学知识求这个问题的解.在解题过程中运用了化二元为一元,化为基本初等函数的数学思想.

练习册系列答案
相关题目
某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为x:3:5.现用分层抽样的方法抽出一个容量为n的样本,样本中A种型号产品有16件,C种型号产品有40件,( )
| A、x=2,n=24 | B、x=16,n=24ks**5u | C、x=2,n=80 | D、x=16,n=80 |