题目内容
为了响应学校“学科文化节”活动,数学组举办了一场数学知识比赛,共分为甲、乙两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的学生中,每组各任选2个学生,作为数学组的活动代言人.
(1)求选出的4个学生中恰有1个女生的概率;(2)设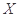 为选出的4个学生中女生的人数,求
为选出的4个学生中女生的人数,求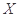 的分布列和数学期望.
的分布列和数学期望.
(1)求选出的4个学生中恰有1个女生的概率;(2)设
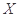 为选出的4个学生中女生的人数,求
为选出的4个学生中女生的人数,求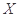 的分布列和数学期望.
的分布列和数学期望.(1)7:15
(2)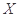 的分布列为
的分布列为
∴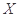 的数学期望
的数学期望
(2)
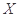 的分布列为
的分布列为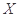 | 0 | 1 | 2 | 3 |
| P |  | 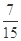 | 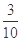 | 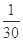 |
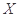 的数学期望
的数学期望
试题分析:解:(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的2个同学中,1个是男同学,1个为女同学”为事件
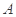 ,“从乙组内选出的2个同学均为男同学;从甲组内选出的2个同学中1个是男同学,1个为女同学”为事件
,“从乙组内选出的2个同学均为男同学;从甲组内选出的2个同学中1个是男同学,1个为女同学”为事件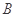 ,由于事件
,由于事件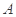 ?
?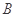 互斥,且
互斥,且
∴选出的4个同学中恰有1个女生的概率为
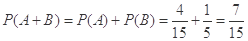 5分
5分(2)
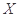 可能的取值为0,1,2,3,
可能的取值为0,1,2,3, 
∴
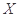 的分布列为
的分布列为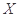 | 0 | 1 | 2 | 3 |
| P |  | 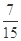 | 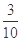 | 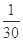 |
∴
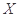 的数学期望
的数学期望 12分
12分点评:主要是考查了分布列的求解以及古典概型概率的计算,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,试写出
,试写出 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的 个题,该考生做对了这
个题,该考生做对了这 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题: 分的概率;
分的概率; ,求
,求 ,则V(X)的值为________.
,则V(X)的值为________. ,则
,则 的值是
的值是  表示取出次品的个数,则
表示取出次品的个数,则 = .
= .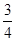 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为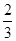 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.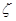 ,求随即变量
,求随即变量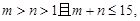
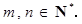 已知从袋中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.现从袋中任取2个球,设取到红球的个数为ξ,则ξ的期望
已知从袋中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.现从袋中任取2个球,设取到红球的个数为ξ,则ξ的期望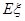 =
=