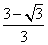题目内容
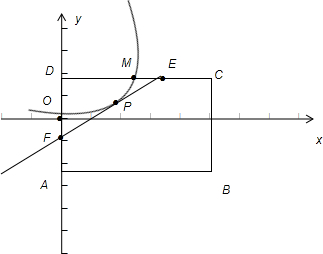
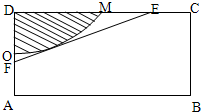
 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?
分析:建立直角坐标系,表示出三角形DEF的面积S△DEF,利用导数判断其单调性可得何时取最小值即得当x=
时,S△EFD取得最小值,相应地,五边形ABCEF的面积最大.
| ||
| 6 |
解答:解:由条件易知边缘线OM是以点D为焦点,直线AB为准线的抛物线的一部分
以O为原点,AD所在的直线为y轴,则D(0,
)M(
,
),易得边缘线OM所在的抛物线方程为:y=x2(0≤x≤
)
要使如图的五边形ABCEF的面积最大,则必有EF所在的直线与抛物线相切,设切点为P(t,t2)则直线EF的方程为y=2t(x-t)+t2即y=2tx-t2由此可求点E,F的坐标分别为E(
,
)F(0,-t2)
∴S△DEF=
×
×(
+t2)=
,t∈(0,
)
∵
=
=
=
显然函数在(0,
]上是减函数,在[
,
]上是增函数,
∴当x=
时,S△EFD取得最小值,相应地,五边形ABCEF的面积最大.
此时点E,F的坐标分别为E(
,
),F(O,-
)
即沿直线EF的线段切割可使五边形ABCEF的面积最大.
以O为原点,AD所在的直线为y轴,则D(0,
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
要使如图的五边形ABCEF的面积最大,则必有EF所在的直线与抛物线相切,设切点为P(t,t2)则直线EF的方程为y=2t(x-t)+t2即y=2tx-t2由此可求点E,F的坐标分别为E(
| 1+4t2 |
| 8t |
| 1 |
| 4 |
∴S△DEF=
| 1 |
| 2 |
| 1+4t2 |
| 8t |
| 1 |
| 4 |
| 16t4+8t2+1 |
| 64t |
| 1 |
| 2 |
∵
| S | ′ △EFD |
| 1 |
| 64 |
| 48t2+8t2-1 |
| t2 |
| (12t2-1)(4t2+1) |
| 64t2 |
=
3(4t2+1)(t+
| ||||||||
| 16t2 |

显然函数在(0,
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
∴当x=
| ||
| 6 |
此时点E,F的坐标分别为E(
| ||
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
即沿直线EF的线段切割可使五边形ABCEF的面积最大.
点评:本题考查通过题意求函数解析式,利用导数判断函数的单调性达到求五边形面积最大值的要求.

练习册系列答案
相关题目
 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米. 缺损了一角(图中阴影部分),边缘线
缺损了一角(图中阴影部分),边缘线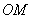 上每一点到点
上每一点到点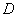 的距离都等于它到边
的距离都等于它到边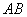 的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若
的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若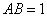 米,
米,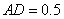 米,当沿切割线
米,当沿切割线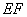 切割使剩余部分五边形
切割使剩余部分五边形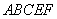 的面积最大时,
的面积最大时,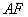 的长度为( )米。
的长度为( )米。 A
A
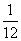 B
B
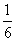
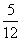 D
D