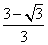题目内容
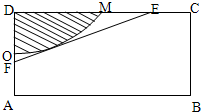 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:边缘线OM上每一点到点D的距离都等于它到边AB的距离.说明边缘线OM是以D为焦点,以AB所在直线为准线的抛物线的一部分,故以AD所在直线为Y轴,以AD的垂直平分线所在直线为x轴,建立坐标系,求得此抛物线的方程,作出如图的切线EF,设出切点的坐标,将五边形的面积表示出来,判断出面积最大时AF的值即为所求,
解答:解:由条件易知,边缘线OM是以点D为焦点,直线AB为准线的抛物线的一部分.以O点为原点,AD所在直线为y轴建立直角坐标系,则p=0.5,易求得边缘线OM所在抛物线的方程为:x2=y…3分
要使如图的五边形ABCEF面积最大,则必有EF所在直线与抛物线相切,设切点为 (x0,y0)
则直线EF的方程为:y-y0=2x0(x-x0),
由此可求得点F、E的坐标分别为(0,-x02),(
,
)
梯形的面积为0.5-
×(
+x0 2)×
=0.5-
×
,x0∈(0,
]
令t=
,x0∈(0,
]
则t′=
=
显然函数t在 (0,
)上是减函数,在 (
,
)上是增函数,
∴当x0=
时,t取得最小值,相应地,五边形ABCEF的面积最大.…12分
此时点E、F的坐标分别为(
,
),(0,-
),
即沿直线EF画线段切割可使五边形ABCEF的面积最大.…13分
要使如图的五边形ABCEF面积最大,则必有EF所在直线与抛物线相切,设切点为 (x0,y0)
则直线EF的方程为:y-y0=2x0(x-x0),
由此可求得点F、E的坐标分别为(0,-x02),(
| ||
| 2x0 |
| 1 |
| 4 |
梯形的面积为0.5-
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 2x0 |
| 1 |
| 64 |
| 16x0 4+8x0 2+1 |
| x0 |
| 1 |
| 2 |
令t=
| 16x0 4+8x0 2+1 |
| x0 |
| 1 |
| 2 |
则t′=
| 48x0 4+8x0 2-1 |
| x0 2 |
12(4x0 2+1)(x0+
| ||||||||
| x0 2 |
显然函数t在 (0,
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
∴当x0=
| ||
| 6 |
此时点E、F的坐标分别为(
| ||
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
即沿直线EF画线段切割可使五边形ABCEF的面积最大.…13分
点评:本题考查抛物线的应用,解题的关键是根据题设条件建立起抛物线模型,再由图形将所研究的面积问题用一个函数关系表示出来,利用函数最值确定两点的坐标定下切线的位置,本题运算量相当大,模型先是建立圆锥曲线模型,再建立切线模型,最后又建立起面积模型,并用导数研究函数的单调性确定出面积取最值时切点的坐标,求出E,F的坐标,运算量大,综合性强,极易出错.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
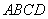 缺损了一角(图中阴影部分),边缘线
缺损了一角(图中阴影部分),边缘线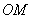 上每一点到点
上每一点到点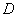 的距离都等于它到边
的距离都等于它到边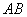 的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若
的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若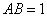 米,
米,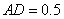 米,当沿切割线
米,当沿切割线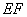 切割使剩余部分五边形
切割使剩余部分五边形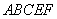 的面积最大时,
的面积最大时,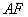 的长度为( )米。
的长度为( )米。 A
A
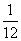 B
B
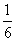
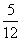 D
D