题目内容
△ABC中,点P满足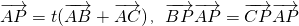 ,则△ABC一定是
,则△ABC一定是
- A.直角三角形
- B.等腰三角形
- C.等边三角形
- D.钝角三角形
B
分析:设D是BC中点,由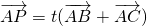 可得点P在三角形ABC的中线AD所在直线上.再由
可得点P在三角形ABC的中线AD所在直线上.再由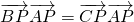 ,可得
,可得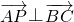 ,从而得到三角形ABC的边BC上的中线与高线重合,可得三角形ABC是等腰三角形.
,从而得到三角形ABC的边BC上的中线与高线重合,可得三角形ABC是等腰三角形.
解答:∵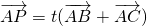 ,设D是BC中点,则
,设D是BC中点,则 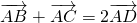 ,
,
∴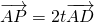 ,故点P在三角形ABC的中线AD所在直线上.
,故点P在三角形ABC的中线AD所在直线上.
∵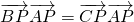 ,∴
,∴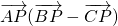 =0,即
=0,即 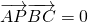 ,即
,即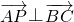 .
.
即 AP⊥BC,故三角形ABC的边BC上的中线与高线重合,
所以,三角形ABC是等腰三角形,其中AB=AC,
故选B.
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的条件,等腰三角形的判定,属于中档题.
分析:设D是BC中点,由
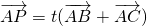 可得点P在三角形ABC的中线AD所在直线上.再由
可得点P在三角形ABC的中线AD所在直线上.再由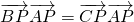 ,可得
,可得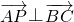 ,从而得到三角形ABC的边BC上的中线与高线重合,可得三角形ABC是等腰三角形.
,从而得到三角形ABC的边BC上的中线与高线重合,可得三角形ABC是等腰三角形.解答:∵
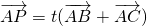 ,设D是BC中点,则
,设D是BC中点,则 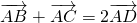 ,
,∴
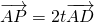 ,故点P在三角形ABC的中线AD所在直线上.
,故点P在三角形ABC的中线AD所在直线上. ∵
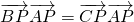 ,∴
,∴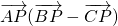 =0,即
=0,即 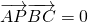 ,即
,即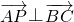 .
.即 AP⊥BC,故三角形ABC的边BC上的中线与高线重合,
所以,三角形ABC是等腰三角形,其中AB=AC,
故选B.
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的条件,等腰三角形的判定,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
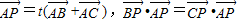 ,则△ABC一定是( )
,则△ABC一定是( )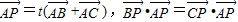 ,则△ABC一定是( )
,则△ABC一定是( )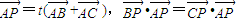 ,则△ABC一定是( )
,则△ABC一定是( )