题目内容
已知点Pn(an,bn)满足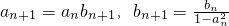 ,且
,且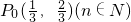 .
.
(1)求点P1坐标,并写出过点P0,P1的直线L的方程;
(2)猜测点Pn(n≥2)与直线L的位置关系,并加以证明;
(3)求数列{an}与{bn}的通项公式(n∈N*).
解:(1)由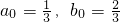 得
得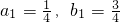 ,得P1坐标为(
,得P1坐标为(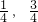 )(2分)
)(2分)
显然直线L的方程为x+y=1(4分)
(2)由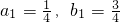 得
得 ,∴点P2∈L,
,∴点P2∈L,
猜想点Pn(n≥2,n∈N)在直线L上,(6分)
以下用数学归纳法证明:
当n=2时,点P2∈L
当n=k(k≥2)时,点Pk∈L,即ak+bk=1,
则当n=k+1时,ak+1+bk+1=akbk+1+bk+1=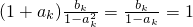 ,
,
∴点Pk+1∈L∴点Pn∈L(n≥2)(11分)
(3)由an+1=anbn+1,bn+1=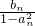 ,an+bn=1
,an+bn=1
得an+1=
∴ (14分)
(14分)
∴ 是等差数列,∴
是等差数列,∴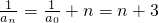 ,
,
∴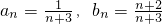 (18分)
(18分)
分析:解:(1)由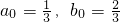 得
得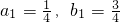 ,得P1坐标为(
,得P1坐标为(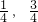 ),最后写出直线L的方程即可;
),最后写出直线L的方程即可;
(2)由条件得出点P2∈L,猜想点Pn(n≥2,n∈N)在直线L上.再利用用数学归纳法证明.
(3)由an+1=anbn+1,得出an+1= 从而得出
从而得出 故有:
故有: 是等差数列,最后根据等差数列的通项公式即可求得数列{an}与{bn}的通项公式.
是等差数列,最后根据等差数列的通项公式即可求得数列{an}与{bn}的通项公式.
点评:本题考查直线的一般式方程、数列递推式、数列和解析几何的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.
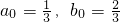 得
得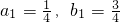 ,得P1坐标为(
,得P1坐标为(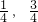 )(2分)
)(2分)显然直线L的方程为x+y=1(4分)
(2)由
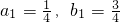 得
得 ,∴点P2∈L,
,∴点P2∈L,猜想点Pn(n≥2,n∈N)在直线L上,(6分)
以下用数学归纳法证明:
当n=2时,点P2∈L
当n=k(k≥2)时,点Pk∈L,即ak+bk=1,
则当n=k+1时,ak+1+bk+1=akbk+1+bk+1=
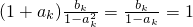 ,
,∴点Pk+1∈L∴点Pn∈L(n≥2)(11分)
(3)由an+1=anbn+1,bn+1=
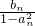 ,an+bn=1
,an+bn=1得an+1=

∴
 (14分)
(14分)∴
 是等差数列,∴
是等差数列,∴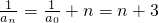 ,
,∴
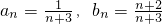 (18分)
(18分)分析:解:(1)由
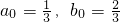 得
得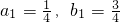 ,得P1坐标为(
,得P1坐标为(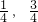 ),最后写出直线L的方程即可;
),最后写出直线L的方程即可;(2)由条件得出点P2∈L,猜想点Pn(n≥2,n∈N)在直线L上.再利用用数学归纳法证明.
(3)由an+1=anbn+1,得出an+1=
 从而得出
从而得出 故有:
故有: 是等差数列,最后根据等差数列的通项公式即可求得数列{an}与{bn}的通项公式.
是等差数列,最后根据等差数列的通项公式即可求得数列{an}与{bn}的通项公式.点评:本题考查直线的一般式方程、数列递推式、数列和解析几何的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目