题目内容
当 时,函数
时,函数 的图象如图所示.
的图象如图所示.(1)求函数f(x)在
 上的表达式;
上的表达式;(2)求方程
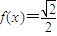 在
在 的解集.
的解集.
【答案】分析:(1)根据图象,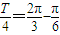 ,可求得ω,利用ω•
,可求得ω,利用ω•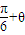 =
=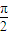 可求得θ,f(0)=
可求得θ,f(0)=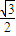 ,可求得A;
,可求得A;
(2)由 可求得其解集.
可求得其解集.
解答:解:(1)∵ ,∴T=2π,ω=1;又
,∴T=2π,ω=1;又 ,∴
,∴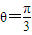 ;由f(0)=
;由f(0)=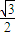 ,得A=1;
,得A=1;
∴ ;
;
(2)由 解得:
解得: .
.
∴方程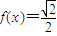 在
在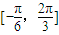 的解集为:
的解集为: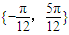 .
.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查其周期,相位,与振幅的确定,属于中档题.
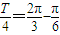 ,可求得ω,利用ω•
,可求得ω,利用ω•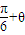 =
=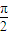 可求得θ,f(0)=
可求得θ,f(0)=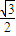 ,可求得A;
,可求得A;(2)由
 可求得其解集.
可求得其解集.解答:解:(1)∵
 ,∴T=2π,ω=1;又
,∴T=2π,ω=1;又 ,∴
,∴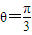 ;由f(0)=
;由f(0)=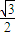 ,得A=1;
,得A=1;∴
 ;
;(2)由
 解得:
解得: .
.∴方程
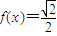 在
在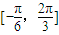 的解集为:
的解集为: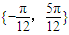 .
.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查其周期,相位,与振幅的确定,属于中档题.

练习册系列答案
相关题目
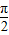 )的图象如图所示.
)的图象如图所示. 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;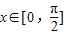 时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.
时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.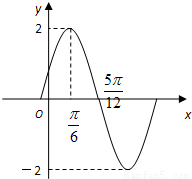
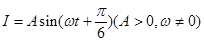 的图象如图所示,则当
的图象如图所示,则当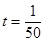 时,电流强度是 。
时,电流强度是 。
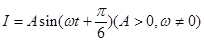 的图象如图所示,则当
的图象如图所示,则当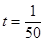 时,电流强度是
。
时,电流强度是
。
 的
的 时,电流强度是
。
时,电流强度是
。