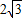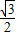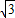题目内容
在△ABC中,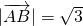 ,
,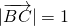 ,sinA=sinB,则
,sinA=sinB,则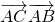 =
=
- A.2
- B.

- C.

- D.

C
分析:由sinA=sinB,根据正弦定理,我们易得a=b,结合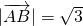 ,
,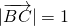 ,我们易得a=b=1,c=
,我们易得a=b=1,c= ,由余弦定理,我们可以求出A的余弦值,代入平面向量数量积的运算公式,得到
,由余弦定理,我们可以求出A的余弦值,代入平面向量数量积的运算公式,得到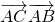 的值.
的值.
解答:∵在△ABC中,sinA=sinB
∴A=B即a=b
又∵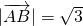 ,
,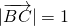
∴a=b=1,c=
则cosA= =
=
∴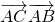 =
=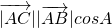 =
=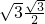 =
=
故选:C
点评:本题考查的知识点是平面向量数量积的运算,根据已知条件△ABC中,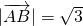 ,
,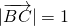 ,sinA=sinB,计算出A的余弦值是解答本题的关键.
,sinA=sinB,计算出A的余弦值是解答本题的关键.
分析:由sinA=sinB,根据正弦定理,我们易得a=b,结合
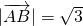 ,
,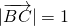 ,我们易得a=b=1,c=
,我们易得a=b=1,c= ,由余弦定理,我们可以求出A的余弦值,代入平面向量数量积的运算公式,得到
,由余弦定理,我们可以求出A的余弦值,代入平面向量数量积的运算公式,得到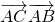 的值.
的值.解答:∵在△ABC中,sinA=sinB
∴A=B即a=b
又∵
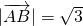 ,
,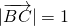
∴a=b=1,c=

则cosA=
 =
=
∴
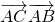 =
=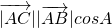 =
=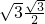 =
=
故选:C
点评:本题考查的知识点是平面向量数量积的运算,根据已知条件△ABC中,
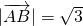 ,
,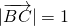 ,sinA=sinB,计算出A的余弦值是解答本题的关键.
,sinA=sinB,计算出A的余弦值是解答本题的关键. 
练习册系列答案
相关题目
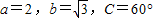 ,则S△ABC=( )
,则S△ABC=( )