题目内容
给定函数① ,②
,② ,③
,③ ,④
,④ ,
,
其中在区间(0,1)上单调递减的函数序号是( )
| A.①② | B.②③ | C.③④ | D.①④ |
B
解析试题分析:因为,幂指数为正,所以,① 是增函数;
是增函数;
因为底数小于1,所以② 是减函数;
是减函数;
因为③ 的图象是关于直线x=1对称的折线,其在(0,1)上是增函数;
的图象是关于直线x=1对称的折线,其在(0,1)上是增函数;
因为底数大于1,所以④ 是增函数;综上知,在区间(0,1)上单调递减的函数序号是②③,故选B。
是增函数;综上知,在区间(0,1)上单调递减的函数序号是②③,故选B。
考点:本题主要考查指数函数、对数函数、幂函数的单调性。
点评:简单题,指数函数、对数函数的单调性,均与底数的取值情况有关,应注意以辨别。

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若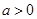 且
且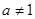 ,且
,且 ,则实数
,则实数 的取值范围( )
的取值范围( )
A.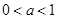 | B. |
C. 或 或 | D.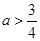 或 或 |
已知函数 ,若
,若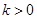 ,则函数
,则函数 的零点个数是
的零点个数是
| A.1 | B.4 | C.3 | D.2 |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
设函数 在点
在点 处连续,则
处连续,则
A. | B. | C. | D. |
函数 的单调递增区间为( )
的单调递增区间为( )
A. | B. | C. | D. |
对数式 有意义,则实数
有意义,则实数 的取值范围是
的取值范围是
| A.(3,4)∪(4,7) | B.(3,7) | C.(-∞,7) | D.(3,+∞) |
设 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
实数 满足
满足 ,则
,则 的值为( )
的值为( )
| A.8 | B. | C.0 | D.10 |