题目内容
某地粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程 =
= x+
x+ .
.
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
 =
= x+
x+ .
.(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
(1)
 =6.5(x-2006)+260.2
=6.5(x-2006)+260.2
(2) 312.2(万吨)
| 年份-2 006 | -4 | -2 | 0 | 2 | 4 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
 =6.5(x-2006)+260.2
=6.5(x-2006)+260.2(2) 312.2(万吨)
【思路点拨】将数据进行处理,方便计算,然后利用公式求回归直线方程,并进行预测.
解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据预处理如下:
由预处理后的数据,容易算得 =0,
=0, =3.2.
=3.2.
 =
= =
=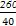 =6.5.
=6.5.
 =
= -
-
 =3.2.由上述计算结果,知所求回归直线方程为
=3.2.由上述计算结果,知所求回归直线方程为 -257=
-257= (x-2006)+
(x-2006)+ =6.5(x-2006)+3.2.
=6.5(x-2006)+3.2.
即 =6.5(x-2006)+260.2.
=6.5(x-2006)+260.2.
(2)利用所求得的直线方程,可预测2014年的粮食需求量为6.5×(2014-2006)+260.2=6.5×8+260.2=312.2(万吨).
解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据预处理如下:
| 年份-2 006 | -4 | -2 | 0 | 2 | 4 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
 =0,
=0, =3.2.
=3.2. =
= =
=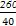 =6.5.
=6.5. =
= -
-
 =3.2.由上述计算结果,知所求回归直线方程为
=3.2.由上述计算结果,知所求回归直线方程为 -257=
-257= (x-2006)+
(x-2006)+ =6.5(x-2006)+3.2.
=6.5(x-2006)+3.2.即
 =6.5(x-2006)+260.2.
=6.5(x-2006)+260.2.(2)利用所求得的直线方程,可预测2014年的粮食需求量为6.5×(2014-2006)+260.2=6.5×8+260.2=312.2(万吨).

练习册系列答案
相关题目
 和
和 的三个散点图,它们从左到右的对应关系依次是( )
的三个散点图,它们从左到右的对应关系依次是( )
 、
、 的取值如下表:
的取值如下表:







 ,则
,则 .
. 算得,
算得, ≈7.8.
≈7.8. ,
, )
)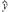 =
= x+
x+ ,求得
,求得 =61.75,
=61.75, =38.14,则线性回归方程为( )
=38.14,则线性回归方程为( ) =9.4x+
=9.4x+ ,当施肥量x=6时,该农作物的预报产量是________.
,当施肥量x=6时,该农作物的预报产量是________. ,
,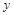 测得一组数据如下表:
测得一组数据如下表: .据此模型预测
.据此模型预测 时,
时, 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )